How to Derive the Equation of Motion for Connected Masses on a Cylinder?

[bobred]

Homework Statement

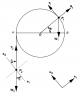
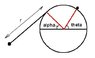
Find the equation of motion, see diagram. Masses are P1 2m and P2 3m.

Homework Equations

Particle 1
$$\texttt{T}_1=\texttt{T}_1\texttt{e}_\theta$$
$$\texttt{N}_1=\texttt{N}_1\texttt{e}_r$$
$$\texttt{W}_1=-2mg\sin\theta{e}_r-2mg\cos\theta{e}_\theta$$

Particle
$$\texttt{T}_2=\sin\theta{e}_r+\cos\theta{e}_\theta$$
$$\texttt{W}_2=-3mg\sin\theta{e}_r-3mg\cos\theta{e}_\theta$$

The Attempt at a Solution

Using Newton's 2nd law $$m\texttt{a}=\texttt{F}$$

P1
$$-2mR\dot{\theta}^2\texttt{e}_r+2mR\ddot{\theta}\texttt{e}_\theta=-2mg\sin\theta{e}_r-2mg\cos\theta{e}_\theta+\texttt{N}_1\texttt{e}_r+\texttt{T}_1\texttt{e}_\theta$$

P2
$$-3mg=\sin\theta{e}_r+\cos\theta{e}_\theta-3mg\sin\theta{e}_r-3mg\cos\theta{e}_\theta$$

Does what I have done look ok? The string is a model string so $$\texttt{T}_1=-\texttt{T}_2$$. How can I find $$\texttt{N}$$ and $$\texttt{T}$$?

 

[hikaru1221]

What's wrong with the dimension of the second equation of P2?
Does the problem provide any initial condition? Under some certain circumstances, the problem may be less complicated.
Let's consider the problem in general case. P2 swings (and maybe goes up or down) and thus, the section connected to P2 in general is not in vertical position. Therefore, in general, the angle coordinate of P2 is not theta.
I suggest a way to look at the problem, though I'm not sure if it's an easy way. The system's position is described by 3 coordinates: theta for P1, alpha and r for P2.

EDIT: I'm sorry, 2 coordinates are enough: theta and either alpha or r.

 

[bobred]

Hi

The system is initially at rest with P1 at B. P2 hangs vertically below A.

For P2 should I be using rectangular components instead of polar.James

 

[hikaru1221]

Okay, so that's much easier. Then the equation for P2 is: $$3mg - T = 3m\ddot{y}$$

We also have this: $$y=R\theta$$

Therefore, $$3mg - T = 3mR\ddot{\theta }$$ (1)

We also have 2 equations for P1:

$$2mR \ddot{\theta }=T-2mgcos \theta$$ (2)

$$2mR \dot{\theta }^2=2mgsin \theta - N$$ (3)

From (1) and (2), get rid of T and do the integration, you will have $$\dot{\theta }(\theta )$$. Combine with (3), you should have $$N(\theta )$$.

Actually if you apply the energy conservation law, things are much easier

 

[bobred]

I take it that P2 has a non-polar coordinate system i.e. x/y?

Thanks

 

[hikaru1221]

Yes, that's the easiest way to analyze P2's motion. In this problem particularly, you even only need 1 coordinate (either x or y) for P2.

 

[bobred]

Thanks, great help.

James

 

[bobred]

Hi

I have completed the question, thanks for your help.
But I'm asked to show that

$$\texttt{N}=\frac{6mg}{5}(3\sin\theta-2\theta)$$

I have integrated and substituted into eqn 3, I get

$$\texttt{N}=2mg\sin\theta-2mR\ddot{\theta}^2$$
$$\texttt{N}=2mg\sin\theta-2mR(\frac{g}{5R}(3\theta-2\sin\theta))$$
$$\texttt{N}=\frac{2mg}{5}(3\sin\theta-3\theta)$$

Can you see where I am going wrong?

Thanks

 

[hikaru1221]

I got the 1st answer. Can you show me your work?

EDIT: I think you got wrong $$\dot{\theta }^2$$
I got: $$\dot{\theta }^2 = \frac{2}{5mR}(3mg\theta - 2mgsin\theta )$$

 

[bobred]

Sorry, I was a bit too hasty, I missed the 2g out, duh!

Thanks

 

[bobred]

Hi

One thing I had forgotten about was the constant of integration, which I have found from the initial conditions of $$\theta=0$$ to be $$\dot{\theta}^2$$. We are also told that the system starts from rest so am I right in thinking that rate of rotation $$\dot{\theta}^2=0$$?

Thanks

 

[hikaru1221]

Yes

 

[bobred]

Thanks for all your help.

James

 

[squinted]

I got the 1st answer. Can you show me your work?

EDIT: I think you got wrong $$\dot{\theta }^2$$
I got: $$\dot{\theta }^2 = \frac{2}{5mR}(3mg\theta - 2mgsin\theta )$$

Hi
Been working thru this problem and I get to here and can't figure out how you arrived at the result.. could you explain it further??
Thanks

 

[bobred]

Using

$$\ddot{\theta}=\dfrac{g}{5R}\left(3-2\cos\theta\right)$$

Whoops, see below.

 

[bobred]

Using

$$\ddot{\theta}=\dfrac{g}{5R}\left(3-2\cos\theta\right)$$ multiply both sides by $$\dot{\theta}$$

Using the fact that $$\dfrac{d}{dt}\left(\dot{\theta}^{2}\right)=2\dot{\theta}\ddot{\theta}$$ insert this into the above equation and integrating both sides gives

$$\dot{\theta}^{2}=\dfrac{2g}{5R}\left(3\theta-2\sin\theta\right)+2c$$

From the given initial conditions c = 0

$$N=2mgsin \theta - 2mR \dot{\theta }^2$$ inserting $$\dot{\theta}^{2}=\dfrac{2g}{5R}\left(3\theta-2\sin\theta\right)$$ into tis equation gives

$$\texttt{N}=\frac{6mg}{5}(3\sin\theta-2\theta)$$

James

 

[squinted]

Thanks James :)