elbowgrease6
- 3
- 0
Homework Statement
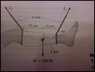
Consider the two cables suspending a leg with a cast in the drawing. If the leg and cast weight 150 N, and the angle of the ankle cable is 60 degrees above the horizontal, what are the cable tensions and the angle of the knee cable from the horizontal such that the leg is supported?
Homework Equations
The Attempt at a Solution
I know it seems simple, but I don't know how to start it. Thank you for any help.