How to determine direction of forces?

[sherrellbc]

I am consistently getting this wrong. To me, in the picture below, it would make sense that the structure would be pulling downward, and the cable BD would be pulling upward - thus the system is in equilibrium.

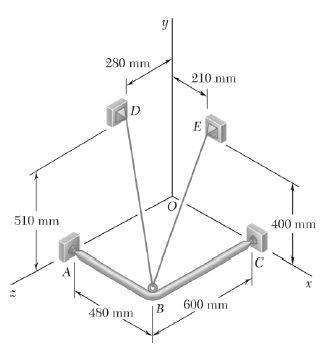
However, the solution to this problem show the force being applied downward onto the structure:

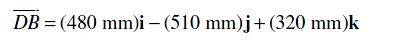
What is the trick?

 

[SteamKing]

DB is not a force. It is measured in mm, so it must be the position vector of point B w.r.t. point D.

B = (480, 0, 600) mm
D = (0, 510, 280) mm

DB = (480, -510, 320) mm

 

[sherrellbc]

I was using the sense of the line to determine the position vector, as you mentioned. I know that DB is not a vector, but if you normalize DB and then multiply the resulting vector by the magnitude of the F along that cable then you effectively have deduced the components of the force.

My problem is that, knowing the force should be from B -> D, I took D-B and got the opposite of what you have shown: DB = (-480, 510, -320).

Given two points, the way you subtract (D-B or B-D) does not matter for the magnitude of the line, but to get an accurate sense of the line you cannot do this action arbitrarily - as I have seen.

I see now though, that the definition of the line is nothing more than determining the LOA of the associated force.