bolzano95
- 89
- 7
- Homework Statement
- The following problem is taken from a physics problem, but I insulated the geometrical part for better understanding.
- Relevant Equations
- α=?
β=?
I'm trying to find angles α and β.
No additional information except: d, h, a.
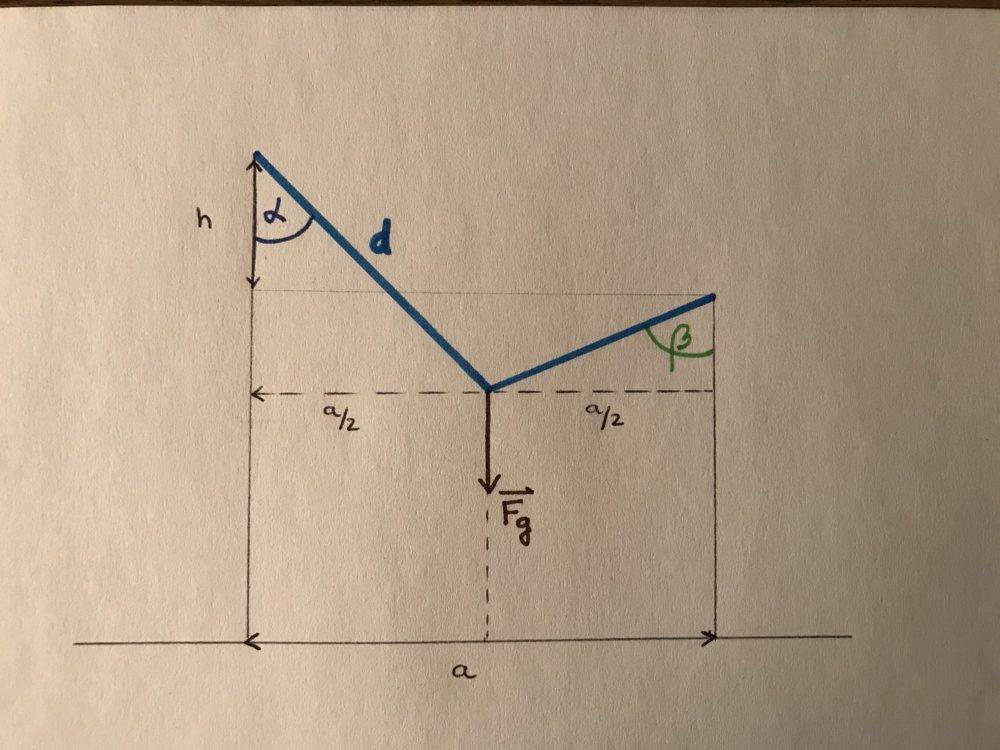
I already tried to figure it out by using isosceles triangles, but this is only true when there is a equilibrium of forces. I thought there are similar triangles incorporated, but I get too many unknown variables and not enough equations. I also tried using trapeziums but it doesn't pan out.
Maybe I overlooked something? Or is there a possibility that this problem is unsolvable?
No additional information except: d, h, a.
I already tried to figure it out by using isosceles triangles, but this is only true when there is a equilibrium of forces. I thought there are similar triangles incorporated, but I get too many unknown variables and not enough equations. I also tried using trapeziums but it doesn't pan out.
Maybe I overlooked something? Or is there a possibility that this problem is unsolvable?

