How to do algebra on the Kitaev toric code grid?

[James1238765]

TL;DR Summary

How to do algebra on the Kitaev toric code grid?

The toric code is a basic computational model as follows:

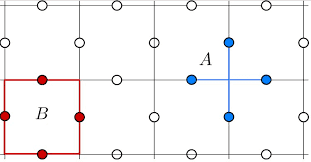
There are 2 operations that can be performed, A and B, on this grid.

To compute the value A at each point on the grid, we transform the raw values at each dot (located in between two vertices) according to some predefined operators $f_a$ and $f_b$, and multiply the four surrounding values from the operations:

$$ A = f_a(left) f_a(up) f_a(right) f_a(down) $$
$$ B = f_b(left) f_b(up) f_b(right) f_b(down) $$

This seems to be a straightforward question, but I could not find a clear answer anywhere.

A commonly used toric code in physics is the model by A. Kitaev (https://www.physics.rutgers.edu/grad/602/Lectures/JC_Presentations/0419/Intro_Toric_Code.pdf)

What confuses me is what type of *quantity* is prescribed at each dot, be it a scalar $0.24$, or a complex number $0.24 + 0.12 i$, or a vector $[0.24, 0.12]$ in this Kitaev toric code model?

Also what is the form of the operator function $f_a$ and $f_b$, be they 2x2 matrices, or something else?

 

[Office_Shredder]

Your source says they're Pauli operators, which I think are 2x2 matrices? From a mathematical standpoint just off your definition real or complex numbers would be fine, but vectors would not be as there is not a standard definition for how to multiply four vectors together (though you could pick a way to do it, e.g. entry by entry multiplication)

Edit to add: in not sure what "Pauli operators acting on individual spins" actually means, but thinking more about the content I think each one is a 2nx2n matrix which is mostly the identity matrix except for a small 2x2 block which is a Pauli matrix.

 

[James1238765]

@Office_Shredder thank you. From what I gather, the dots are spinors, represented by the |0> and |1>, so I suppose that usually translates to:

$$
|1> = \begin{bmatrix}
0 \\
1
\end{bmatrix} ,
|0> = \begin{bmatrix}
1 \\
0
\end{bmatrix}
$$

The A and B operators seem to be the Pauli matrices:

$$ f_a =
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix},

f_b =
\begin{bmatrix}
1 & 0 \\
0 & -1
\end{bmatrix}
$$

So I suppose the operation goes something as follows:

$$f_a(|1>) =
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}
\begin{bmatrix}
0 \\
1
\end{bmatrix} =
\begin{bmatrix}
1 \\
0
\end{bmatrix}
$$

Supposing that's are correct, how then do we multiply the four resulting column vectors together?

$$f_a(left) f_a(up) f_a(right) f_a(down)= ? $$

And then, the final answer for A seems to be a scalar. But how do 4 vector multiplications result in a scalar answer? It's quite mysterious.

 

[Office_Shredder]

We can start by noting that Av and Bp are
Hermitian and square to the identity

What makes you think these are scalar? $f_a(left)$ is an operator, and you multiply four of them together to get another operator. I think each of these operators is an operator on a large dimensional space, which (for the Z's and X's in the paper, $f_a(x)$ and $f_b(y)$ in your notation) is the identity everywhere except is a Pauli matrix on some specific subspace.

 

[James1238765]

@Office_Shredder Yes you're right, those are operators! So,

$$ A = f_a(f_a(f_a(f_a(|1>)))) = f_a(f_a(f_a(|0>))) = f_a(f_a(|1>)) = f_a(|0>) = |1>$$
$$ B = f_b(f_b(f_b(f_b(|0>)))) = f_b(f_b(f_b( -|0>))) = f_b(f_b(|0>)) = f_b( -|0>) = |0> $$

So the final answers are likely closed within the set {|0>, |1>, -|0>, -|1>}.

The next step is to calculate S, being the total sum of A over every square on the grid, and the sum of B over every square on the grid.

$$ S = \sum_{grid} A - \sum_{grid} B $$

This S would also be a single column vector, with integer real number values for each component like $S = \begin{bmatrix} -10 \\ 7 \end{bmatrix}$ , do you think?

 

[Office_Shredder]

No, for two reasons. 1.) Why are you applying the operator to a state? An operator can just exist, and they can be multiplied and added. 2.) It says the spin state of each node is being tracked separately. So your state vector is actually going to be very large, not a vector of length 2.

 

[James1238765]

@Office_Shredder I suspect it's the Kronecker product of each of the 4 operation

$$f_a(left) \otimes f_a(up) \otimes f_a(right) \otimes f_a(down)$$

where $f_a$ is $\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$ for dots surrounding the point in question, and $\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$ for all other points?

from [here]

 

[Office_Shredder]

No. Each $f_a(x)$ is already an operator defined on the large state of all spins. At that point you just do normal matrix multiplication.

The matrix representation of each $f_a$ is conceptually similar to what you described for a single 2x2 block, except kronecker products are more complicated (recall the dimension of the spaces grows multiplicatively as you add more products, not linearly) so it's better to just keep everything in tensor product form the whole time and not try to write down a matrix.

 

[James1238765]

@Office_Shredder Do you mean for a 100x100 grid, $f_a$ is defined as an entire Kronecker product of the whole grid, something like a 100x100 sized matrix? This huge matrix is calculated once at the beginning of the simulation, and all subsequent calculation is just normal matrix multiplication?

Apologies if it looks like I'm splitting hairs over the minute details. The goal is to implement and time evolve the grid, and I usually can't do it if even a small part of the model is left vague, as I need to implement every step of the model.

If you have understood the whole thing, it might be easier to just give an explicit and concrete numerical example how to calculate A at a grid point (which is what the texts should probably have done in place of their roundabout definitions).

 

[Office_Shredder]

No, the matrix will be $2^{10,000}$ by $2^{10,000}$ which is why they are not writing things down as matrices and you shouldn't either.

Remember how kronecker products work. Suppose I have three spin states, and each one has a 2 dimensional basis $e_0$ and $e_1$. Then the product has a basis of dimension 8, i.e $2^3$
$e_0 \otimes e_0 \otimes e_0$,
$e_0 \otimes e_0 \otimes e_1$,
$e_0 \otimes e_1 \otimes e_0$,
$e_1 \otimes e_0 \otimes e_0$,
$e_0 \otimes e_1 \otimes e_1$
$e_1 \otimes e_0 \otimes e_1$,
$e_1 \otimes e_1 \otimes e_0$,
$e_1 \otimes e_1 \otimes e_1$

In your case you have roughly $10,000$ spin states. The actual set of allowed matrices is small though.

 

[James1238765]

In the related Ising model of spin lattice behavior, spin is represented as scalar 2-valued quantity {1, -1} representing up and down spin. This model is a kind of cellular automaton with the following rules.

Consider a point on the grid $[x, y]$. This point has a current spin, let's call it 1 (up).

Give this point $[x,y]$ a current total score, by comparing this point with its immediate left neighbor. If the spin the same, add 1 to the score. If the spin is opposite, subtract 1from the score. Compare with its up, right, down neighbors the same way. The total score for this specific gridpoint $[x,y]$ at current time can range from {-4, -3, -2, -1, 0, 1, 2, 3, 4} depending on the different current states of its neighbors.

Then compute a hypothetical score in the same manner, but supposing that the spin is now reversed, ie. suppose that spin = -1 (down).

If the hypothetical score is better (higher) than the current score, immediately flip the spin of this gridpoint and be done with current task.

If the hypothetical score is worse (lower) than the current score, we could simply forbid the spin to flip altogether. It is more common though to be magnanimous and give it a minuscule change $\frac{1}{e^{score deficit}}$ of switching its spin even though the score will in fact get worse. If the score difference is 1, the chance of overturning the spin is $\frac{1}{e^1} = 37\%$. If the score difference is 2, the chance of overturning the spin is $\frac{1}{e^2} = 13\%$. The chances drops to $5\%$ and $2\%$ for opposing the spins of a maximum all 4 neighbors of this point.

A steady state (with some background fluctuations) is obtained, when the initial population of spin 1 and spin -1 grid values are 50-50.

(red = spin 1, yellow = spin -1)

 

[Paul Colby]

Hi, something seems off with this discussion, perhaps not. If I may, the paper models a system of spin-$\frac{1}{2}$ particles interacting along the spin $z$-direction only. Each spin is associated with an edge. The system state space is the tensor product of all the spins 2D spaces. If there are $N$ spins then the operators, $A_v$ and $B_p$, are $2N\times 2N$ matricies. In fact the $A_v$ and $B_p$ are all diagonal since only $\sigma_z$ for each spin is used.

 

[James1238765]

@Paul Colby thank you. I guess the $\otimes$ is what's been throwing me off all this while, as I have not encountered something like it before.

Let's calculate A at a point $A_{100}$, with its neighbors being left= $[1,0]$, up=$[0,1]$, right=$[1,0]$, down=$[0,1]$.

The X operator for A is the matrix
$$X = \begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}$$.

How should we compute the plaquette operation $A_{100} = \sigma_{left} \sigma_{up} \sigma_{right}\sigma_{down}$ from here?

How should we compute the sum $\sum_{grid} A_n$ over all grid points, and what on earth is being Kroneckered $\otimes$?

 

[Office_Shredder]

Hi, something seems off with this discussion, perhaps not. If I may, the paper models a system of spin-$\frac{1}{2}$ particles interacting along the spin $z$-direction only. Each spin is associated with an edge. The system state space is the tensor product of all the spins 2D spaces. If there are $N$ spins then the operators, $A_v$ and $B_p$, are $2N\times 2N$ matricies. In fact the $A_v$ and $B_p$ are all diagonal since only $\sigma_z$ for each spin is used.

The paper says the Hilbert space has dimensions $2^{2L^2}$ which I think agrees with my interpretation and not yours.

 

[Paul Colby]

reply under review

 

[Paul Colby]

The paper says the Hilbert space has dimensions $2^{2L^2}$ which I think agrees with my interpretation and not yours.

Yeah, I think I agree here. A 2 spin system has 4 states and a three spin system 8, not 6 Like what I just posted again.

 

[Paul Colby]

Okay, Office_Shredder gave the proper way to form the state space for a three spin system in #10.

Let $Z_k$ be the operator for the z-component of spin index $k$. This operator acts only on the k-th spin independent of all other spins. These spins are fermions so all spin components of spin k anti commute with every other spin, $$Z_kZ_j=-Z_jZ_k$$ whenever $k\ne j$. All $A_v$ commutes with every other $A_v$ because they are even products of anti commuting operators. The $B_p$ operators are constructed using the $X_k$ components. $Z_k$ definitely does not commute with $X_k$ so checking that $A_v$ commutes with all the $B_p$ needs to be shown.

The matrices associated with these operators are immense but the algebra they obey is straightforward.

 

[Office_Shredder]

The matrices associated with these operators are immense but the algebra they obey is straightforward.

I really want to emphasize this. For a 100 by 100 grid you have an algebra of about 20,000 matrices where you can write down exactly how each product of matrices works in a couple sentences. If you want to represent them as matrices by their definition you need like, more numbers than there are atoms in the universe. So you definitely should not do that.

 

[James1238765]

Thank you @Paul Colby @Office_Shredder . I am still working this out, but I like math forums for this reason. Let's talk about math without other baggage. If it's alright I would post other math modeling questions in this sub forum.