How to explain TE20 mode in a rectangular waveguide from reflection

[Dale12]

In Feynman's lectures, he explained the $TE_{10}$ mode of waveguide by considering a line source in the middle of waveguide as below:

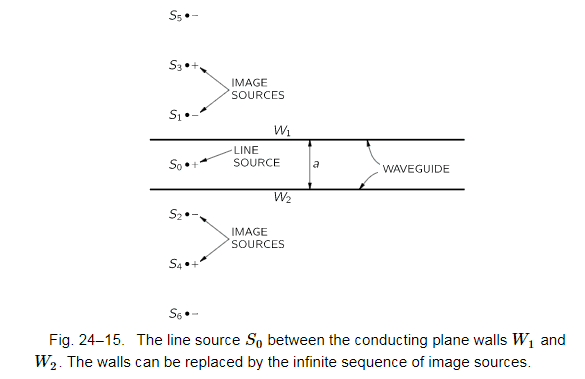
since the adjacent sources are all out-of-phase, which means to have interference, the adjacent optical path would be about half of wavelength as below:

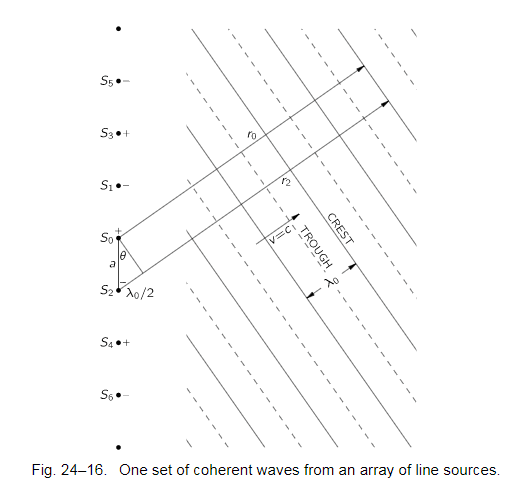
where
$$\sin\theta = \frac{\lambda_0}{2a}$$ (24.33)

and the relationship between wavelength in waveguide and free-space is show in this picture:

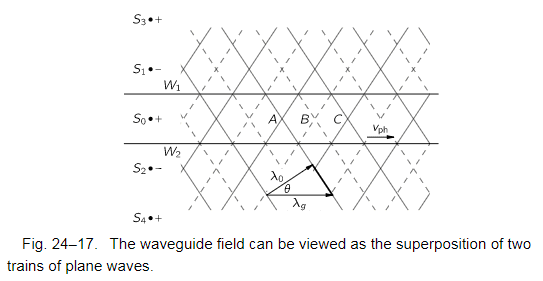
and we have:
$$\cos\theta = \frac{\lambda_0}{\lambda_g}$$,

combing with $\sin\theta = \frac{\lambda_0}{2a}$, we have:

$$\lambda_g = \frac{\lambda_0}{\cos\theta} = \frac{\lambda_0}{\sqrt{1-(\lambda_0/2a)^2}}$$

Feynman then summarized with:
“ If the frequency is high enough, there can be two or more possible directions in which the waves will appear. For our case, this will happen if $\lambda_0<\frac{2}{3}a$. In general, however, it could also happen when $\lambda+0<a$. These additional waves correspond to the higher guide modes we have mentioned. ”

However, $\lambda_0<\frac{2}{3}a$ is corresponding to $TE_{30}$ modes and the differential phase between adjacent source is about 3/2 wavelength, but how to explain $\lambda+0<a$ which corresponding to one wavelength or $TE_{20}$ mode?

Thanks!

 

[Dale12]

And also it seems work for TE modes of parallel plate waveguide, but it seems hard to explain TM modes of parallel plate waveguide.

 

[Dale12]

I think I have make it clear now.
Q1: I think $TE_{20}$ mode can't be generated by putting a line source in the middle of wavguide, because the distribution of electric field for the $TE_{20}$ mode at a/2 is zero, in order to generate $TE_{20}$ mode, we can put the line source in the place of a/4, and mirror the source in the same way as Feynman does.

Q2: I think the line source can't generate the TM mode for the parallel plate waveguide, however, we can explain TE and TM both in view of incident and reflection from the PEC border of waveguide, and then for E components parallel to PEC, the reflection should have an -1, so that it has a form of sin function to be standing wave, and it's similar for H components perpendicular to PEC. for E components perpendicular and H components parallel to PEC, we have the same phase of reflection and then a standing wave of form cos function.