EggEgg
- 2
- 0
Homework Statement
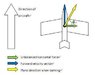
An aircraft remains in flight by generating a force, called Lift, which acts to counter gravity. By design, Lift always acts in the “up” direction of the aircraft frame of reference (i.e., orthogonally to a lateral axis along the wings). An aircraft turns by banking its wings, thereby changing the direction of the Lift force. The diagram to the right illustrates this.
To maintain level flight, the Lift force must increase, so that the vertical component of lift balances gravity. In this situation though there is an unbalanced horizontal turning force, which causes the aircraft to turn in a circle.
Q.1 Determine the lift force, L, required to counter gravity, as a function of the bank angle,\theta
Q.2 Use the above information to determine a function relating the speed of the aircraft and the bank angle to the turning radius (i.e., the radius of the circle inscribed by the aircraft during the turn).
Homework Equations
N/A
The Attempt at a Solution
I have answered Q.1 as:
In bank angle\theta=0, lift force L is equal to gravity g, thus:
(L cos)\theta=g
\theta=cos-1(g/L)
For Q.2
I know i can use bank angle to find out horizontal force, and use forward velocity with this force to find out the turning angle, but i don't know how to find out the radius with these information