jkristia
- 54
- 0
One of the questions in the homework for online precalc class I'm taking is to find the exact value for cos (67.5).
At first I didn't realize that I should just take the half angle of 135, so instead I tried to find the value for cos (45 + 45/2), and got stuck at this point.
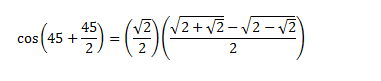
If I calculate the actual value I get the correct answer, but I'm not able to see how I can simplify this further.
I know the solution is as simple as finding the half angle value of
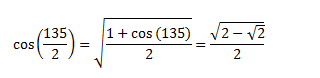
Any suggestions of how I can get from my first attempt solution to the simpler (and correct) solution?
At first I didn't realize that I should just take the half angle of 135, so instead I tried to find the value for cos (45 + 45/2), and got stuck at this point.
If I calculate the actual value I get the correct answer, but I'm not able to see how I can simplify this further.
I know the solution is as simple as finding the half angle value of
Any suggestions of how I can get from my first attempt solution to the simpler (and correct) solution?