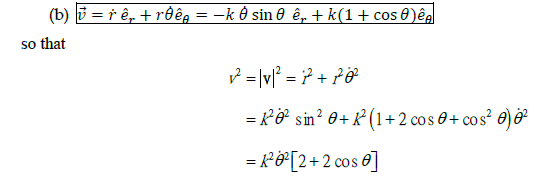How to find the length of a vector expressed in polar coordinates?

[Tony Hau]

The velocity of a particle below is expressed in polar coordinates, with bases e r and e theta. I know that the length of a vector expressed in i,j,k is the square of its components. But here er and e theta are not i,j,k. Plus they are changing as well. Can someone help convince me that the length of v is still the square of its components?

 

[PeroK]

Either use the orthonormality of $\hat r, \hat \theta$. Or, convert the vector to Cartesian coordinates to double check.

 

[Gaussian97]

Well, first of all answer this question, what are the scalar products of
$$\hat{e}_r\cdot\hat{e}_r, \qquad \hat{e}_r\cdot\hat{e}_\theta, \qquad \hat{e}_\theta\cdot\hat{e}_\theta$$

 

[Tony Hau]

Well, first of all answer this question, what are the scalar products of
$$\hat{e}_r\cdot\hat{e}_r, \qquad \hat{e}_r\cdot\hat{e}_\theta, \qquad \hat{e}_\theta\cdot\hat{e}_\theta$$

e r dot e r is (e r)^2
e r dot e theta is 0
e theta dot e theta is (e theta)^2

 

[Gaussian97]

And what are the values of $\hat{e}_r^2$ and $\hat{e}_\theta^2$?

 

[Tony Hau]

And what are the values of $\hat{e}_r^2$ and $\hat{e}_\theta^2$?

Both are 1?

 

[Gaussian97]

Exact! Now you can compute directly what is the product
$$v^2 = \vec{v}\cdot \vec{v}$$

 

[Tony Hau]

My guess is like this. The dot product of v itself will make both bases vanish. So the dot product is just the square of its components.

 

[Gaussian97]

Yes, essentially is this, although it's good to make the computation once in your life :)

 

[Tony Hau]

Either use the orthonormality of $\hat r, \hat \theta$. Or, convert the vector to Cartesian coordinates to double check.

May I confirm that if a vector is expressed in orthonormal bases, they will have the same operation as if they are expressed in the standard bases? It is because I got another HW question asking the cross product of two vectors expressed in spherical coordinates.

 

[PeroK]

May I confirm that if a vector is expressed in orthonormal bases, they will have the same operation as if they are expressed in the standard bases? It is because I got another HW question asking the cross product of two vectors expressed in spherical coordinates.

For the cross product you also have to think about the right-handedness of your basis vectors. Not just the orthonormality.

 

[Tony Hau]

For the cross product you also have to think about the right-handedness of your basis vectors. Not just the orthonormality.

Sorry I only learned how to determine the right-hanedness of standard bases. How can you determine the right-handedness of other basis vectors?

 

[PeroK]

Sorry I only learned how to determine the right-hanedness of standard bases. How can you determine the right-handedness of other basis vectors?

With your right hand! It's the same idea.

 

[Gaussian97]

Sorry I only learned how to determine the right-hanedness of standard bases. How can you determine the right-handedness of other basis vectors?

It's the same idea as the scalar product. To compute the scalar product in one base you need to know the scalar product of the basis vectors $\hat{e}_i\cdot\hat{e}_j$. Then to compute the vector product of a vector you need to know first the vector product $\hat{e}_i\times\hat{e}_j$. To be right-handed simply means $\hat{e}_i\times\hat{e}_j = \varepsilon_{ijk}\hat{e}_k$

 

[Tony Hau]

It's the same idea as the scalar product. To compute the scalar product in one base you need to know the scalar product of the basis vectors $\hat{e}_i\cdot\hat{e}_j$. Then to compute the vector product of a vector you need to know first the vector product $\hat{e}_i\times\hat{e}_j$. To be right-handed simply means $\hat{e}_i\times\hat{e}_j = \varepsilon_{ijk}\hat{e}_k$

Thanks for your reply

 

[vanhees71]

Let's go through the logic of polar coordinates to summarize what has been achieved nicely above:

It's a simple example for curvilinear orthogonal coordinates. You start from a cartesian basis $\vec{e}_1$ and $\vec{e}_2$. Then you define polar coordinates $(r,\theta)$ with $r \in \mathbb{R}_{>0}$ and $\theta \in ]-\pi,\pi]$ (of course you can define the angle to be in any semi-open interval of length $2 \pi$) as
$$\vec{r}=x \vec{e}_1+ y \vec{e}_2=r \cos \theta \vec{e}_1 + r \sin \theta \vec{e}_2.$$
Then it's also convenient to define, at each point, a basis system given by the tangent vectors of the coordinate lines, i.e., the lines given by holding one of the two polar coordinates constant:
$$\vec{b}_r=\partial_r \vec{r}=\cos \theta \vec{e}_1 + \sin \theta \vec{e}_2, \quad \vec{b}_{\theta}=\partial_{\theta} \vec{r}=-r \sin \theta \vec{e}_1 + r \cos \theta \vec{e}_2.$$
It's easy to see that
$$\vec{b}_r \cdot \vec{b}_{\theta}=0,$$
i.e., that the two tangent vectors on the coordinate lines at any point are orthogonal to each other. In this case, usually one chooses the basis for the curvilinear coordinates as normalized. Now $\vec{b}_r^2=1$ and $\vec{b}_{\theta}^2=r^2$. Thus we define
$$\vec{e}_r=\vec{b}_r = \cos \theta \vec{e}_1 + \sin \theta \vec{e}_2, \quad \vec{e}_{\theta}=\frac{1}{r} \vec{b}_{\theta} = -\sin \theta \vec{e}_1 + \cos \theta \vec{e}_2.$$
Now you have at any point a orthonormal basis system since
$$\vec{e}_{r}^2=\vec{e}_{\theta}^2=1, \quad \vec{e}_r \cdot \vec{e}_{\theta}=0.$$
Now as with any basis you can define vector components with respect to this "curvilinear bases". In your case this was done for the velocity vector. To that end just use the original Cartesian coordinates first and then express the resulting vectors in terms of the new basis vectors:
$$\vec{v}=\dot{\vec{r}}=\mathrm{d}_t (r \cos \theta \vec{e}_1 + r \sin \theta \vec{e}_2) = \dot{r} \vec{e}_r + r \dot{\theta} \vec{e}_{\theta}.$$
Thus you have the components
$$v_r=\dot{r}, \quad v_{\theta}=r \dot{\theta}.$$
Now, since these are components with respect to an orthronormal basis, you get
$$\vec{v}^2=(v_r \vec{e}_r + v_{\theta} \vec{e}_{\theta})^2=v_r^2 \vec{e}_r^2 + v_{\theta}^2 \vec{e}_{\theta}^2 + 2 v_r v_{\theta} \vec{e}_r \cdot \vec{e}_{\theta}=v_r^2 + v_{\theta}^2 = \dot{r}^2 + r^2 \dot{\theta}^2.$$