Discussion Overview
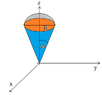
The discussion revolves around finding the volume of a cone and a hemisphere using spherical coordinates. Participants explore the mathematical relationships and volume calculations involved in this geometric problem.
Discussion Character
- Mathematical reasoning
- Technical explanation
- Exploratory
Main Points Raised
- Some participants express uncertainty about the limits of the radius \( r \) for the cone and hemisphere, suggesting ranges such as \( 0 < r < R \) for the hemisphere and \( 0 < r < R \csc(\theta) \) for the cone.
- One participant provides a detailed calculation for the height of the cone based on the angle \( \theta \), concluding that \( h = \sqrt{3} R \) when \( \tan(30^\circ) = \frac{R}{h} \).
- Participants calculate the volume of the cone as \( V = \frac{\sqrt{3} \pi R^3}{3} \) and the volume of the hemisphere as \( V = \frac{2 \pi R^3}{3} \), leading to a total volume of \( V = \frac{(2 + \sqrt{3}) \pi R^3}{3} \).
- Another participant questions how to find the volume if the surface equation is defined with \( [\cos(\theta)]^2 \), indicating a potential shift in the approach to the problem.
- One participant challenges the relevance of surface equations to volume calculations, emphasizing the distinction between surface area and volume.
Areas of Agreement / Disagreement
Participants generally agree on the formulas for the volumes of the cone and hemisphere but express differing views on the limits of integration and the relevance of surface equations to volume calculations. The discussion remains unresolved regarding the implications of the surface equation.
Contextual Notes
Participants have not reached a consensus on the limits of the radius \( r \) for the cone, and there are unresolved questions about the relationship between surface equations and volume calculations.