- #1
yuiop
- 3,962
- 20
It is often stated that the one way speed of light cannot be measured and that the isotropic speed of light is just an assumption based on two way measurements and clock synchronisation conventions.
Here is a proposal for measuring the one way speed of light. It is not entirely original as it is based on the method used by Ole Romer to make this measurement by observing eclipses of Jupiter's moon Io, but is slightly simplified and idealised for easy analysis.
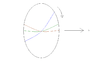
First we require a radial arm of length r. One end of the arm is anchored to an axis and the other end is free. A single clock is placed at A on the circumference of the arms arc. The arm is rotated to a high velocity v. A signalling flash device is placed at B on the opposite side of the circle. Each time the arm passes B the flash is triggered. The tangential velocity of the free end of the arm is computed as 2*pi*r/T, where T is the time to complete one full circle as measured by the clock at A. When the arm is rotating at a steady high velocity, some reading are taken. Let's say when the arm passes A the time is t1. The time t2 of the flash when the arm passes B, as measured by the clock at A when it receives the signal, is (pi*r/v)+(2*r/c) which includes the light travel time.
The one way speed of light is obtained by solving for c which is c=2*r/(t2-t1-pi*r/v) or 2*r/(t2-t1-T/2).
Now because the one way speed of light is often disputed, there may be some hidden tautologies in the above thought experiment. Can anyone say what they think they are?
Here is a proposal for measuring the one way speed of light. It is not entirely original as it is based on the method used by Ole Romer to make this measurement by observing eclipses of Jupiter's moon Io, but is slightly simplified and idealised for easy analysis.
First we require a radial arm of length r. One end of the arm is anchored to an axis and the other end is free. A single clock is placed at A on the circumference of the arms arc. The arm is rotated to a high velocity v. A signalling flash device is placed at B on the opposite side of the circle. Each time the arm passes B the flash is triggered. The tangential velocity of the free end of the arm is computed as 2*pi*r/T, where T is the time to complete one full circle as measured by the clock at A. When the arm is rotating at a steady high velocity, some reading are taken. Let's say when the arm passes A the time is t1. The time t2 of the flash when the arm passes B, as measured by the clock at A when it receives the signal, is (pi*r/v)+(2*r/c) which includes the light travel time.
The one way speed of light is obtained by solving for c which is c=2*r/(t2-t1-pi*r/v) or 2*r/(t2-t1-T/2).
Now because the one way speed of light is often disputed, there may be some hidden tautologies in the above thought experiment. Can anyone say what they think they are?
Last edited: