How to measure the time dependent correlation of two signals

[vibe3]

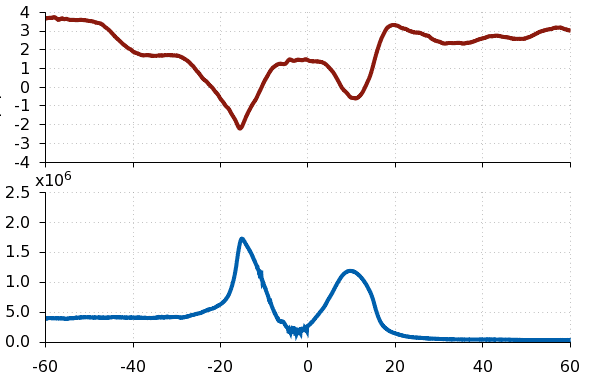
I have two signals (time series) shown in the plot below. Just by looking at the figure, we can see that the two main peaks of both signals are very closely aligned (correlated), however the red signal has additional features elsewhere which don't match the blue curve.

I am looking for some function which can tell me how correlated these two signals are at a given time. IE: at t = -18 and t = +10 where the peaks are located, the correlation should be very close to -1, while at t = -40, the correlation is probably close to 0.

Specifically, I want a robust way to tell that if I see a peak in the blue curve, then there is a corresponding (negative) peak in the red curve.

I've looked into cross correlation (https://en.wikipedia.org/wiki/Cross-correlation), however this seems suitable for time series which simply have a constant time lag with respect to each other. In my problem the correlation between my two signals is changing with time. I've thought about dividing up the signal into small bins and computing the correlation of each bin, but I was hoping there is a better way.

 

[andrewkirk]

They look pretty correlated to me. Note that correlation does not mean identical. From the graphs it appears that you could model the relationship perfectly well with a constant correlation and a noise term.

If you want a model with a time-varying correlation you could use a system of three stochastic DEs, one for the first time series, one for the second, which contains a correlation term to the first, and one for the randomly time-varying correlation which could for instance be an Ito process with mean-reversion to an equilibrium of zero (Ornstein-Uhlenbeck process). But it would be complicated to calibrate, and not necessarily stable.

 

[vibe3]

They look pretty correlated to me. Note that correlation does not mean identical. From the graphs it appears that you could model the relationship perfectly well with a constant correlation and a noise term.

If you want a model with a time-varying correlation you could use a system of three stochastic DEs, one for the first time series, one for the second, which contains a correlation term to the first, and one for the randomly time-varying correlation which could for instance be an Ito process with mean-reversion to an equilibrium of zero (Ornstein-Uhlenbeck process). But it would be complicated to calibrate, and not necessarily stable.

Yes that is a nice example which has a good correlation. However, I have lots of examples where there is no corresponding peak in the red curve. Or sometimes there is 2 peaks in the blue curve but only 1 peak in the red curve. This is why I need a time-varying correlation.

My current thinking is to use a peak-finding algorithm to find the 2 peaks in the blue curve. Then isolate the same time intervals in the red curve and use a normal correlation on just the region near the peak. This way I can detect if both peaks are correlated, or just 1 peak, or 0 peaks

 

[FactChecker]

It sounds like you are trying to change the model completely from on time to another, not just get a "time changing correlation". That is fine if you have a logical reason to propose different models at different times. Otherwise, you may not have a valid basis for your conclusions.