How to pronounce a nuclear reaction written in AZE notation?

[spareine]

Pronouncing a nuclear reaction like

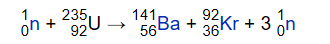
as "one,zero,neutron + 235,92,uranium yields 141,56,barium + 92,36,krypton + 3,1,0,neutron" is awkward. How is it pronounced by physicists in practice?

 

[mfb]

"Neutron plus Uranium 235 reacts to Barium 141, Krypton 92 and 3 neutrons"
"Uranium 235 gets fissioned by a neutron to Barium 141, Krypton 92 and 3 neutrons"
With colleagues working on the same topic, the element names might get replaced by their short forms.

The element fixes the proton number, and "neutron" is clear as well.

 

[e.bar.goum]

The reason that you don't normally pronounce the Z is that it's implicit in the element name. Saying both is redundant. "neutron induced fission of uranium 235 yields barium 141 and krypton 92 along with 3 neutrons" or something like that.

In some countries, saying "235 uranium" is more common (A first). This isn't exactly wrong but I have a strong preference for the other way around.