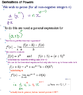You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How to prove the derivatives of powers?
- Thread starter Owen-
- Start date
-
- Tags
- Derivatives
Physics news on Phys.org
Owen-
- 40
- 0
Hmm instead of just taking the linear part of the binomial expansion, why wasn't the full thing written down? Surely If the full formula for binomial was written out it would prove what we wanted?
the (x^n) parts would cancel then the only term without h in it after you divide across by h you would be left with what you wanted...
the (x^n) parts would cancel then the only term without h in it after you divide across by h you would be left with what you wanted...
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,119
- 138
Well.
You would need to make an explicit error estimate to show that the rest term goes to zero sufficiently fast, but that is quite easy.
Another way of doing this is by assuming the truth of the product rule, and prove the general formula by induction:
Assume
f_{k}(x)=x^{k}, f_{k}^{'}(x)=k*x^{k-1}
Note that this formula is true for k=1.
For arbitrary "k", we wish to prove that the formula holds for "k+1" as well:
f_{k+1}(x)=x^{k+1}=x*f_{k}(x)\to{f}_{k+1}^{'}(x)=1*x^{k}+x*k*x^{k-1}=(k+1)*x^{k}
Therefore, we have proved that the formula holds for all powers k.
You would need to make an explicit error estimate to show that the rest term goes to zero sufficiently fast, but that is quite easy.
Another way of doing this is by assuming the truth of the product rule, and prove the general formula by induction:
Assume
f_{k}(x)=x^{k}, f_{k}^{'}(x)=k*x^{k-1}
Note that this formula is true for k=1.
For arbitrary "k", we wish to prove that the formula holds for "k+1" as well:
f_{k+1}(x)=x^{k+1}=x*f_{k}(x)\to{f}_{k+1}^{'}(x)=1*x^{k}+x*k*x^{k-1}=(k+1)*x^{k}
Therefore, we have proved that the formula holds for all powers k.
Owen-
- 40
- 0
So the only thing my lecturer needed to do there was to
? And it would have been proven?show that the rest term goes to zero sufficiently fast
arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,119
- 138
Yes, in an epsilon-deltawise manner.
Rather tedious and longwinded; that's why he didn't bother to do it.
Rather tedious and longwinded; that's why he didn't bother to do it.
Owen-
- 40
- 0
Ah - ok, thanks! Any chance you could find a link to this proof?
Frankly i don't even know what to look for :S
Thanks again,
Owen.
Frankly i don't even know what to look for :S
Thanks again,
Owen.
hunt_mat
Homework Helper
- 1,798
- 33
Try this proof:
<br /> f'(a)=\lim_{x\rightarrow a}\frac{x^{n}-a^{n}}{x-a}<br />
But x^{n}-a^{n} has a factor of x-a, then we can factorise.
<br /> x^{n}-a^{n}=(x-a)(x^{n-1}+ax^{n-2}+\cdots +xa^{n-2}+a^{n-1})<br />
Then from here the limit is easy to find and the result follows.
<br /> f'(a)=\lim_{x\rightarrow a}\frac{x^{n}-a^{n}}{x-a}<br />
But x^{n}-a^{n} has a factor of x-a, then we can factorise.
<br /> x^{n}-a^{n}=(x-a)(x^{n-1}+ax^{n-2}+\cdots +xa^{n-2}+a^{n-1})<br />
Then from here the limit is easy to find and the result follows.
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 984
I don't believe that is the point they are making. They have, though some details have been jumped over, proved that the derivative of x^n is n x^{n-1} for n any positive integer. When they say "this is true in general", I think that they mean that it is true for n any number, not just a positive integer.
The most direct way to prove that the derivative of x^a is ax^{a- 1} for a any number is to use logarithms.
If y= x^a then y= e^{ln(x^a)}= e^{a ln(x)}. Assuming that you already know that the derivative of e^x is e^x, the derivative of ln(x) is 1/x, and the chain rule (which is why they "haven't proved it yet"), then we can say
\frac{dy}{dx}= \left(e^{aln(x)}\right)\left(\frac{a}{x}\right)
And, now, since e^{a ln(x)}= e^{ln(x^a)}= x^a, that says that
\frac{dy}{dx}= x^a\frac{a}{x}= ax^{a-1}.
The most direct way to prove that the derivative of x^a is ax^{a- 1} for a any number is to use logarithms.
If y= x^a then y= e^{ln(x^a)}= e^{a ln(x)}. Assuming that you already know that the derivative of e^x is e^x, the derivative of ln(x) is 1/x, and the chain rule (which is why they "haven't proved it yet"), then we can say
\frac{dy}{dx}= \left(e^{aln(x)}\right)\left(\frac{a}{x}\right)
And, now, since e^{a ln(x)}= e^{ln(x^a)}= x^a, that says that
\frac{dy}{dx}= x^a\frac{a}{x}= ax^{a-1}.
Similar threads
- Replies
- 12
- Views
- 6K
- Replies
- 2
- Views
- 3K
- Replies
- 17
- Views
- 3K
- Replies
- 7
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 4
- Views
- 1K
- Replies
- 0
- Views
- 2K
- Replies
- 5
- Views
- 2K
Hot Threads
-
I Understanding Legendre differential equation
- Started by chwala
- Replies: 2
- Differential Equations
-
I Visual Representation of Separation of Varables
- Started by sonnichs
- Replies: 4
- Differential Equations
-
A Searching for radial part solution of Klein-Gordon type equation
- Started by art1915
- Replies: 1
- Differential Equations
-
I Why Lagrange’s method of solving Pp + Qq=R works?
- Started by PLAGUE
- Replies: 3
- Differential Equations
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math