How to prove Theta for a incline plane.

[aj-smith]

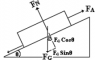
In physics class, we always assumed both theta's. Can someone prove to me why the angle for gravity is the same as the angle of the inclined plane? I can clearly see that triangles could be created and visually they look similar, but obviously that isn't enough.

Image is in the attachment.

Thanks

 

[goodcow]

If you draw down the lines for force from the point where the box touches the ramp, everything becomes much clearer. Two right angles are created: one at the flat base of the ramp and one at the point where the box touches the ramp. The triangle with the original θ is completed by an angle with value 90-θ. Since the place where the box touches the ramp has a right angle, that is then θ.

 

[aj-smith]

So just because the triangle at the block is a right angle, the angle closest to the block is considered theta?

I see the part of 90-θ, but how do you match that with the opposing angle to theta in the 2nd triangle to make the assumption that that angle that is at the block is theta?

Sorry that I am not seeing it, yet I must say thanks for the reply.