It can be solved using contour integration . The approach is quite long I might post it later .
On the other hand we can transform to another contour integration using a substitution .
$$t = \frac{1}{x}-1 \,\,\, dt = - \frac{1}{x^2}dx$$
$$\int^{\infty}_0 \frac{dt}{ \sqrt[3]{t}(t+1)}$$
we can use the following function to integrate
$$f(z) = \frac{e^{\frac{-1}{3}\text{Log}_0(z)}}{z+1}$$
Notice we are choosing a branch cut along the positive x-axis .
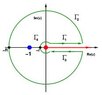
We will use a key-hole contour as indicated in the picture .
View attachment 909
$$\oint_{\Gamma_2} f(z) \, dz +\oint_{\Gamma_4} f(z) \, dz+ \int_{\Gamma_3} f(z) \, dz + \int_{\Gamma_1} f(z) \, dz = 2\pi i \text{Res}(f(z) ; -1) $$
Integration along the big circle :
$$\oint_{\Gamma_2}\frac{e^{\frac{-1}{3}\text{Log}_0(z)}}{z+1}\, dz $$
We will use the following paramaterization $$z = Re^{it}\,\,\, 0< t < 2\pi $$
$$iR\int_{0}^{2\pi }\frac{e^{it}\, e^{\frac{-1}{3}\text{Log}_{0}(Re^{it})}}{Re^{it}+1}\, dt \leq 2 \pi \frac{R^{1-\frac{1}{3}}}{R-1} $$
Now take $R$ to be arbitrarily large
$$\lim_{R \to \infty}2 \pi \frac{R^{\frac{2}{3}}}{R-1} = 0 $$
Similarity the integration along the smaller circle goes to $0$ as $$r \to 0$$ .
Integration along the x-axis :
$$\text{P.V} \int^{\infty}_{0} \frac{e^{\frac{-1}{3}\text{Log}_0(z)}}{z+1}\, dz $$
Along the positive x-axis we get the following
$$\text{P.V} \int^{\infty}_{0} \frac{e^{\frac{-1}{3}\ln(x)}}{x+1}\, dx$$
For the other integral on the opposite direction
$$\text{P.V} \int^{0}_{\infty} \frac{e^{\frac{-1}{3}(\ln(x)+2\pi i)}}{x+1}\, dx$$
The residue at $$-1$$
Since we have a simple pole
$$\text{Res}(f;-1)= e^{-\frac{1}{3}\text{Log}_0(-1)} = e^{-\frac{\pi}{3} i} $$
Final step
$$\text{P.V}(1-e^{-\frac{2\pi}{3} i } )\int^{\infty}_{0} \frac{1}{\sqrt[3]{x}(x+1)}\, dx = 2\pi i e^{-\frac{\pi}{3} i} $$
$$\text{P.V}\int^{\infty}_{0} \frac{1}{\sqrt[3]{x}(x+1)}\, dx = 2\pi i \frac{e^{-\frac{\pi}{3} i}}{1-e^{-\frac{2\pi}{3} i } } $$
We can easily prove that $$2\pi i \frac{e^{-\frac{\pi}{3} i}}{1-e^{-\frac{2\pi}{3} i } }=\frac{\pi }{\sin \left( \frac{\pi}{3}\right)}=\frac{2\pi }{\sqrt{3}}$$
Hence the result
$$\text{P.V}\int^{\infty}_{0} \frac{1}{\sqrt[3]{x}(x+1)}\, dx = \frac{2\pi }{\sqrt{3}} $$
We can easily prove that the integral converges hence the principle value is equal to the integral $$\square$$ .