TheMarksman
- 7
- 0
Hi guys,
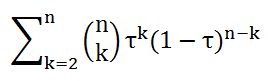
I am a little confused about how to interpret the matrix included in the equation...can someone please write it in a single line not using the matrix for let's say n=3...
Thanks in advance.
I am a little confused about how to interpret the matrix included in the equation...can someone please write it in a single line not using the matrix for let's say n=3...
Thanks in advance.