peguerosdc
- 28
- 7
(Throughout all my post, I will refer to “gravitational potential energy” just as “potential energy”)
Hi! I have this confusion about when is potential energy positive/negative and how it is related to how we define our axes. I think it is easier to understand my confusion with the following examples:
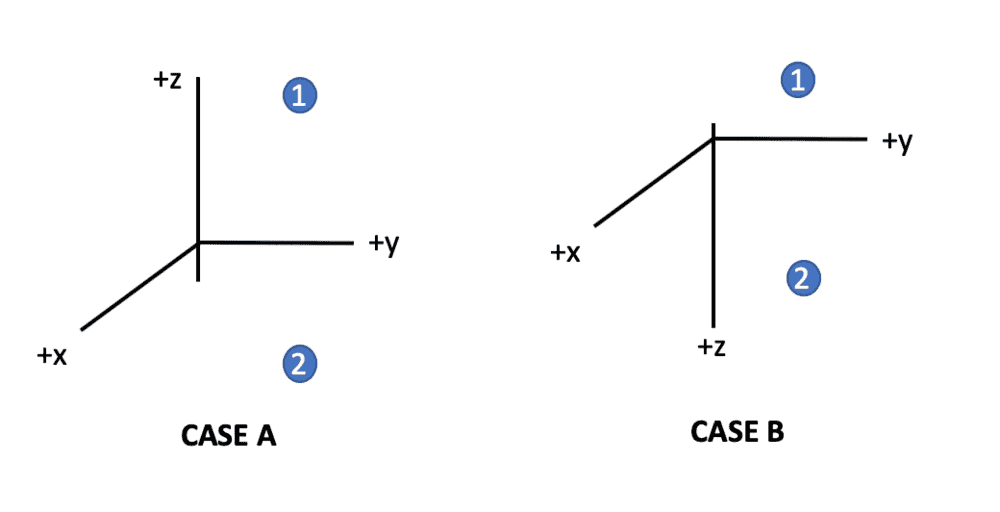
In case A, I have defined my axes to be as shown in the picture, with +z pointing up (x and y really don’t matter in my example). Suppose gravity points down (so it is in the direction of negative z) and that there is a particle (a blue ball) somewhere in the 3D plane.
As this is the most common set-up according to all the examples I have seen, I would define the potential energy as ##U = mgz## where the zero reference is where all the axes intersect. In this set-up, if particle is at position 1, the potential energy would be positive and if it as position 2, it would be negative.
My confusion is in case B, where I have defined my positive z axis pointing down keeping the zero reference at the intersection of the axes and the gravitational force pointing down (which in this case would be in the +z direction). In this case, should the potential energy be defined as ##U = mgz## or ##U = -mgz## ?
What I think:
If the object is above the zero reference, its potential energy must be positive and if it is below, it should be negative, independently of how the axes are defined.
So, based on this, I think the correct answer is ##U = - mgz## because:
Hi! I have this confusion about when is potential energy positive/negative and how it is related to how we define our axes. I think it is easier to understand my confusion with the following examples:
In case A, I have defined my axes to be as shown in the picture, with +z pointing up (x and y really don’t matter in my example). Suppose gravity points down (so it is in the direction of negative z) and that there is a particle (a blue ball) somewhere in the 3D plane.
As this is the most common set-up according to all the examples I have seen, I would define the potential energy as ##U = mgz## where the zero reference is where all the axes intersect. In this set-up, if particle is at position 1, the potential energy would be positive and if it as position 2, it would be negative.
My confusion is in case B, where I have defined my positive z axis pointing down keeping the zero reference at the intersection of the axes and the gravitational force pointing down (which in this case would be in the +z direction). In this case, should the potential energy be defined as ##U = mgz## or ##U = -mgz## ?
What I think:
If the object is above the zero reference, its potential energy must be positive and if it is below, it should be negative, independently of how the axes are defined.
So, based on this, I think the correct answer is ##U = - mgz## because:
- If the particle is above the reference (at position 1), “z” would be negative, which would make U positive, agreeing with my assumption.
- If the particle is below the reference (at position 2), “z” would be positive, which would make U negative, agreeing with my assumption.