noid
- 8
- 0
I have started with the formula.
T = 0.5q+4q^(-1/2)+9/q
I have derived and am trying to solve for q but have gotten caught up on how to solve when I have to subtract two variables with different base numbers and different exponents.
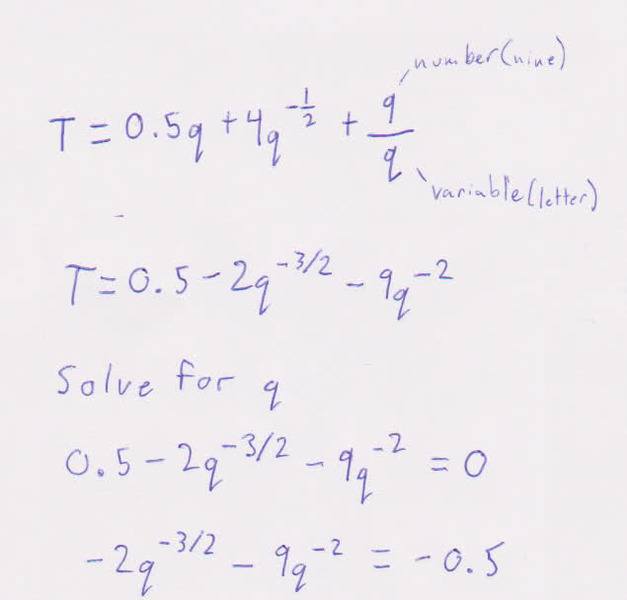
Any ideas?
T = 0.5q+4q^(-1/2)+9/q
I have derived and am trying to solve for q but have gotten caught up on how to solve when I have to subtract two variables with different base numbers and different exponents.
Any ideas?
Last edited: