Regtic
- 75
- 3
I was solving this problem

and I didn't want to do it the really long way by finding the equation of B(t) by first finding T(t) and N(t). So i took the cross product of r' and r'' so that they would be in the direction of B. Found the parametric equation of the plane but the book answer was in the general format.
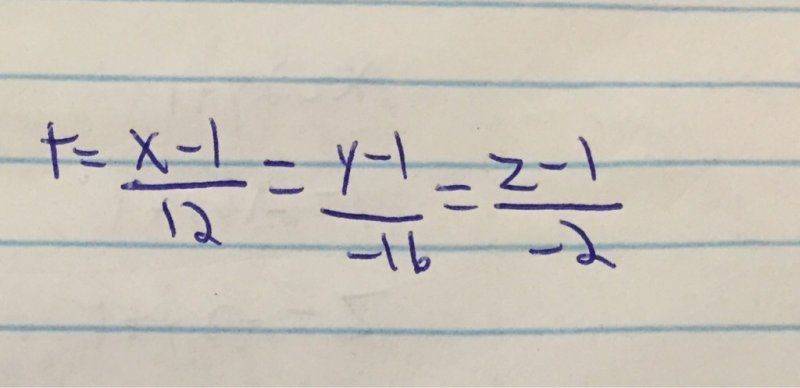
How do I turn this into the general format to check my answer? It should be 2X +Y +4Z -7 = 0
Whenever I try i just get two equations that don't mix to give me x y and z in one equation but it should be right.
and I didn't want to do it the really long way by finding the equation of B(t) by first finding T(t) and N(t). So i took the cross product of r' and r'' so that they would be in the direction of B. Found the parametric equation of the plane but the book answer was in the general format.
How do I turn this into the general format to check my answer? It should be 2X +Y +4Z -7 = 0
Whenever I try i just get two equations that don't mix to give me x y and z in one equation but it should be right.
Last edited: