- #1
- 1,866
- 34
My problem is how to understand this problem. I am confident that I can solve it, but I need to know what they mean in the problem.
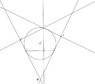
"[PQ] is a chord of a circle. R lies on the major arc of the circle."
I understand this.
"Tangents are drawn through P and through Q."
What does this mean? I would say that they meant that there are tangents touching the circle in P and Q.
"From R, perpendicuars [PA], [PB] and [PC] are drawn to the tangent at A, the tangent at B and [AB] respectively."
I'm totally lost. What do they mean with this?
"Prove that [tex]RA.RB=RC^2[/tex]"
This is the problem I am to prove, when I understand the problem.
Basic geometry theorems
Just need some help with understanding the problem.
Thanks
Homework Statement
"[PQ] is a chord of a circle. R lies on the major arc of the circle."
I understand this.
"Tangents are drawn through P and through Q."
What does this mean? I would say that they meant that there are tangents touching the circle in P and Q.
"From R, perpendicuars [PA], [PB] and [PC] are drawn to the tangent at A, the tangent at B and [AB] respectively."
I'm totally lost. What do they mean with this?
"Prove that [tex]RA.RB=RC^2[/tex]"
This is the problem I am to prove, when I understand the problem.
Homework Equations
Basic geometry theorems
The Attempt at a Solution
Just need some help with understanding the problem.
Thanks
Last edited: