How to understand the Bloch sphere in the quantum computation?

[Haorong Wu]

I've read that $\left | \psi \right > =cos \frac \theta 2 \left | 0 \right > + e^{i \phi} sin \frac \theta 2 \left | 1 \right >$, and the corresponding point in the Bloch sphere is as the fig below shows.

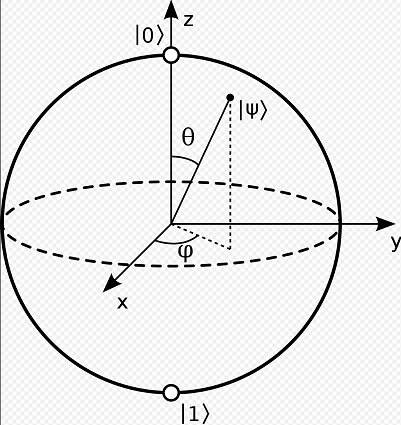
I think $\left | 0 \right >$ and $\left | 1 \right >$ are orthonormal vectors, then why they seem to apear parallel in the Bloch sphere?

Also, I can understand the $cos \frac \theta 2 \left | 0 \right >$ part, but I cannot understand how $e^{i \phi} sin \frac \theta 2 \left | 1 \right >$ part can match the fig.

Thanks!

 

[DrClaude]

Consider a spin-1/2 particle. The two eigenvalues of $S_z$ are $\pm \hbar/2$, which correspond to opposite points along $z$. The fact that $|+z\rangle$ and $|-z\rangle$ are orthogonal states must not be confused with the orthogonality of the cartesian axes.

Likewise, consider that
$$
|\pm x \rangle = \frac{1}{\sqrt{2}} \left( |+z \rangle \pm |-z \rangle \right) \\
|\pm y \rangle = \frac{1}{\sqrt{2}} \left( |+z \rangle \pm i |-z \rangle \right)
$$
This is exactly what is transposed to the Bloch sphere.

 

[cosmik debris]

I think $\left | 0 \right >$ and $\left | 1 \right >$ are orthonormal vectors, then why they seem to apear parallel in the Bloch sphere?

Spin half particles take 720 degrees to return to their original state.

Cheers