Hydrostatics: U-Tube Homework Solution

[Darth Frodo]

Homework Statement

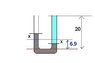
A u-tube of uniform cross section with vertical limbs of height 20cm has mercury of relative density 13.6 in the bottom of it. The columns of mercury in each limb are 6.9cm high. Water is poured into one limb until it just reaches the top. Find the height of the water column.

Homework Equations

P = \rhogh

The Attempt at a Solution

Please find attached.

Please excuse the massive x. I got angry.

 

[ehild]

Your picture is good, but I would put the reference at the bottom line.

There is 6.9 cm +x height of mercury in the left limb of the U-tube, and (6.9-x) cm height of mercury +h cm height of water in the right one. The length of both vertical limbs is 20 cm, the right limb is filled with water to the top, the height of the water column +the height of mercury is 20 cm: h+(6.9-x)=20 cm. The pressure is equal in both limbs at the reference line (the red one in my picture)..

It is said that the relative density of mercury is 13.6 - given with respect to the density of water. No need to convert the densities to kg/m³. If you do it, convert also cm to m.

Your error was that you multiplied everything when calculated the pressure in the right limb. The pressure of the water column is added to that of the mercury.


ehild

 

[Darth Frodo]

EXCELLENT! Thanks very much, this is extremely helpful!