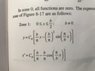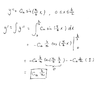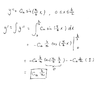The discussion centers on the confusion regarding the integration of the second derivative, y'', to obtain the first derivative, y'. Participants clarify the difference between definite and indefinite integrals, emphasizing that indefinite integrals yield antiderivatives while definite integrals result in numerical values. The original poster struggles with the textbook's approach, particularly why the integration is expressed in terms of a variable x rather than a fixed limit like b/2. The conversation highlights the necessity of boundary conditions for determining constants of integration and the importance of understanding the context of definite versus indefinite integrals. Ultimately, the clarification helps resolve the misunderstanding about the integration process in the context of the problem.