I have a few questions for my Phys Lab

[scissors]

1.) I have a diagram of a simple circuit, a square wave generator (Vin) a resistance R, and capacitance C.

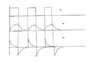
Then the square wave function of Vin vs t (10^-4 sec) is shown.

Vo starts at a max, goes down at 0.5 stays down till 1.0, and then goes up to the max, goes down at 1.5.

Now I have R = 1 kOHMs an C = .01 microFarads, and I am to sketch a graph of Vc versus time and Vr versus time over these same intervals.

I am using the equation Vc = Vo(1-e^-t/RC), but is this correct for a square wave? And what is the equation for Vr? My notes don't have one, but I'm sure it would be somewhat similar to Vc.

I have a second question, but I'm going to try to read my notes once again before posting that. Once again, thanks for any assistance!

 

[Curious3141]

Your question is not that clear, and there's no diagram. I'm assuming the square wave varies between 0 and a max value of V_0 with a period of 1 unit of time (I think you mean that's 10^{-4} seconds, right ? The equation you gave for V_C is correct, but it applies only to the period when the total voltage is at V_0. When the total voltage drops "instantly" to zero, the voltage across the capacitor decreases exponentially with formula V_t = V'_0e^{-\frac{t}{RC}}. Note that V'_0 is strictly not the same as V_0 because an ideal capacitor "never" becomes fully charged (or discharged) in finite time.

V_R is given by V_R + V_C = V_0 when the total voltage is at V_0 and by V_R + V_C = 0 when the applied voltage goes to zero.

Try sketching a graph and attaching it here and I (or someone else) will critique it.

 

[scissors]

Thanks for that equation. I'm waiting for my friend to wake up so that I can scan in the sheets, but meanwhile, I'm pretty stumped on the second part.

____

If the square wave generator above is replaced with a sine wave generator with amplitude Vo, at what frequency, fc of the voltage Vc across the capacitor equal to Vo/sqrt(2)?

What is the magnitude Zc of the impedance of the capacitor at this frequency?

At this frequency what is the phase of the voltage across the capacitor relative to the input signal from the generator?

At this frequency what is the magnitude of the voltage across the resistor, and what is its phase relative to the input signal from the generator?

I'm just looking for a way to start these problems. I have all the equations, but I'm not sure what a good first step is. Any help is greatly appreciated!

For the first one, I tried setting "1-e^-t/RC" = 1/sqrt(2)

but I wasn't sure...

 

[Curious3141]

Thanks for that equation. I'm waiting for my friend to wake up so that I can scan in the sheets, but meanwhile, I'm pretty stumped on the second part.

____

If the square wave generator above is replaced with a sine wave generator with amplitude Vo, at what frequency, fc of the voltage Vc across the capacitor equal to Vo/sqrt(2)?

What is the magnitude Zc of the impedance of the capacitor at this frequency?

At this frequency what is the phase of the voltage across the capacitor relative to the input signal from the generator?

At this frequency what is the magnitude of the voltage across the resistor, and what is its phase relative to the input signal from the generator?

I'm just looking for a way to start these problems. I have all the equations, but I'm not sure what a good first step is. Any help is greatly appreciated!

For the first one, I tried setting "1-e^-t/RC" = 1/sqrt(2)

but I wasn't sure...

I'm sorry, but with that last equation, you're totally on the wrong track.

Have you covered basic a.c. circuit analysis ? Do you know how how to use complex numbers to represent phasors and impedances ? Then we can go from there.

 

[scissors]

Ah thanks. I haven't done much with impedance before, today will be the first lab of the semester, and I do have the equation

Zc = -i / WC

 

[Curious3141]

Ah thanks. I haven't done much with impedance before, today will be the first lab of the semester, and I do have the equation

Zc = -i / WC

Fantastic. We can go from there.

A note first. Learn to use j rather than i when you mean \sqrt{-1} in Physics, at least in circuit analysis, lest you confuse it with current. It is the accepted convention.

So you should write :

Z_C = \frac{1}{j\omega C} = \frac{-j}{\omega C}

The first part of the question :

at what frequency, fc of the voltage Vc across the capacitor equal to Vo/sqrt(2)?

is poorly phrased. It should be rephrased to "...is the amplitude of the voltage across the capacitor..." since the voltage across the cap. is continuously varying. This is in fact what the question means.

Consider what happens when two known simple resistances are placed in series and connected to a voltage source, as in a voltage divider. What is the expression of the voltage across one of the resistors ?

You can treat the complex expression for Z_C exactly like a resistance (only you call it a reactance, or impedance). The resistance of the resistor, of course, is R and is a real value.

Use the same expression as in the voltage divider to express V_C in terms of the total voltage V. You now have \frac{V_C}{V} as a complex expression. Now set the magnitude of that complex expression to \frac{1}{\sqrt{2}} and see what you get for \omega. You should easily be able to find an expression for the frequency from the value of \omega.

See if you can handle the rest, else I'll help.

 

[scissors]

Oh yeah, you were right about the time...I meant 10^-4.

The scans are small for some reason, but here they are.

Questions[/URL]

The graph is the first one, and the second two are for me to write in.

Below is what I think it should be

[PLAIN]Answer[/URL]

The first one is VC, the second one is Vr and the graph has the interval +vo to - Vo

 

[scissors]

Ah, thanks a lot! I have now

Vc = -j/wC Ioe^jwt

But how do I obtain an expression for V itself? Is that an eqn in terms of Vc and Vr?

 

[Curious3141]

Oh yeah, you were right about the time...I meant 10^-4.

The scans are small for some reason, but here they are.

Questions[/URL]

The graph is the first one, and the second two are for me to write in.

Below is what I think it should be

[PLAIN]Answer[/URL]

The first one is VC, the second one is Vr and the graph has the interval +vo to - Vo[/QUOTE]

The questions image came out OK, it was what I expected.

The answers image didn't come out so clearly, but I'm afraid it's quite obviously wrong, it doesn't have the right "shape" at all.

Here's what the answer should look like. My artwork is terrible, but you should get an idea. In case the captions are difficult to read, the top one is the total voltage (square wave), the middle one is the voltage across the capacitor, the bottom one is the voltage across the resistor.

 

[Curious3141]

Ah, thanks a lot! I have now

Vc = -j/wC Ioe^jwt

But how do I obtain an expression for V itself? Is that an eqn in terms of Vc and Vr?

You don't actually need to bring the current into it at all, if you handle everything as complex impedances and the overall picture as a voltage divider.

 

[scissors]

AH, thanks for the graphs, they were helpful, and made sense.

I guess for the impedance, I am having trouble obtaining the equations to divide by.

 

[Curious3141]

AH, thanks for the graphs, they were helpful, and made sense.

I guess for the impedance, I am having trouble obtaining the equations to divide by.

I have to catch some shut eye, but here's the way I would do the first part :

\frac{Z_C}{Z_C + R} = \frac{V_C}{V}

\frac{\frac{1}{j\omega C}}{\frac{1}{j\omega C} + R} = \frac{V_C}{V}

Simplifying,

1 + j\omega R C = \frac{V}{V_C}

Taking the magnitude of both sides,

({1 + {\omega}^2R^2C^2})^{\frac{1}{2}} = \frac{|V|}{|V_C|} = \frac{V_0}{|V_C|}

We want \frac{V_0}{|V_C|} to be \sqrt{2}, so :

1 + {\omega}^2R^2C^2 = 2

giving \omega = \frac{1}{RC}

and f = \frac{1}{2\pi RC}

'Kay ?

 

[scissors]

Thanks a LOT! Haha, you are a lifesaver. I tried doing it some random way but I wasn't sure.