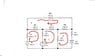
omni said:
well when you told that" what i can do is assign a variable, say Vx to the voltage across the current source, and add another constraint equation. The new constraint imposes the relationship between current B and C that is forced by the current source. "
can you show me what will need to be the another constraint equation ?
and should i ignore the equations that i wrote before ?
For the constraint equation, look at what currents are flowing in the branch between loops B and C. What must the sum of the mesh currents in that branch be?
Your equations will have to be modified in order to accommodate the new constraint. The equations for loops A and D should remain the same, I think.
mean this equations :
500a-100b-200c-100d=0
-100a+300b-100c-0d=100
-200a-100b+400c-100c=0
-100a-0b-100c+300d=-100
If you recognize that the current through R3
must be 1A (flowing upward), how might your equations for loops B and C change? And if the current source has an unknown potential difference Vx, how will they change? Once you've massaged those two loop equations to include the effects of the current supply you can eliminate Vx by solving for it on one of the two equations and substituting the result into the other.
As a result you will have "used up" the information in one equation to get rid of the new variable Vx. That's why you need the new constraint equation, to keep the number of equations available equal to the number of unknowns to solve.
i know there is a method to solve it with matrix, if i want to use it i need to change all the voltage source to a current source, and then in every cross-road (-1cross-road) i need to mark Va,Vb,...
and then to write the matrix.
but if i do it here i get 4 variable and i don't know yet how to solve this kind of matrix,(only with 3 variable i know).
so if you can show me what will need to be the another constraint equation is can be helpful.
thanks.
Yes, that would be nodal analysis. It solves for the voltages at the nodes in the circuit rather than currents in the branches. It uses KCL at each node, and you can fill in the matrix 'automatically' using conductances rather than resistances.
But you've got four loops and so four currents to solve for in the mesh approach, and four nodes in the nodal analysis approach, so they seem at first glance to be of equal difficulty. But in the node method the node voltage at the top of the current source branch is fixed by the current source and the branch resistor, so that node's voltage is already 'solved'. You end up with one less equation (leaving three)!