- #1
mathfriends
- 7
- 0
[URL]http://www13.0zz0.com/2011/07/15/22/754178270.jpg[/URL]
I Need help solving this fourth degree equation
I Need help solving this fourth degree equation
Last edited by a moderator:
Me, too.I want answers
HallsofIvy said:The simplest way to approach this problem is to use the "rational root theorem".
Why don't you tell us? Are those answers the same as the ones you already know:mathfriends said:this is another solution
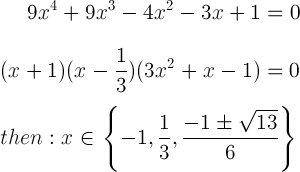
Is this true ?
mathfriends said:thank you
FinallyI found a solution
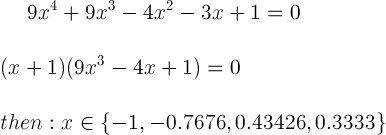
Redbelly98 said:Why don't you tell us? Are those answers the same as the ones you already know:
mathfriends said:this is another solution
Is this true ?
I like Serena said:What do you think?
Can you think of a way to derive this solution?
Btw, are you familiar with solving a quadratic equation?
That is, an equation of the form ax2 + bx + c = 0.
HallsofIvy said:The simplest way to approach this problem is to use the "rational root theorem".
If r is a rational number satisfying [itex]a_nx^n+ a_{n-1}x^{n-1}+ \cdot\cdot\cdot+ a_1x+ a_0= 0[/itex] where the coefficients are all integers, then r= p/q where p is an integer evenly dividing [itex]a_0[/itex] and q is an integer evenly dividing [itex]a_n[/itex].
Of course, it is not necessary than such an equation have any rational roots but it is worth trying. Here, the leading coefficient, [itex]a_n[/itex], is 9, which has factors [itex]\pm 1, \pm 3, \pm 9[/itex] and the constant term, [itex]a_0[/itex] is 1, which has factors [itex]\pm 1[/itex] so the only possible rational roots are [itex]\pm 1, \pm 1/3, \pm 1/9[/itex].
Putting those into the equation, we see that if
[tex]9(1)^4+ 9(1)^3- 4(1)^2- 3(1)+ 1= 19- 7= 12\ne 0[/tex]
[tex]9(-1)^4+ 9(-1)^3- 4(-1)^2- 3(-1)+ 1= -9+ 9- 4+ 3+ 1= -1+1= 0[/tex]
[tex]9(1/3)^4+ 9(1/3)^3- 4(1/3)^2- 3(1/3)+ 1= 1/9+ 1/3- 4/9- 1+ 1= 1/3- 1/3- 1+ 1= 0[/tex]
We can stop here. Seeing that x= -1 and x= 1/3 are roots, we can divide by x+ 1 and x- 1/3 (not "0.3333") to get a quadratic equation that we can solve using the quadratic formula.
(There is a "quartic formula", http://www.sosmath.com/algebra/factor/fac12/fac12.html, but it is extermely complicated.)
A fourth degree equation is an algebraic equation that contains a variable raised to the fourth power, such as ax4 + bx3 + cx2 + dx + e = 0. These types of equations can have up to four distinct solutions or roots.
The most common method for solving a fourth degree equation is by using the rational roots theorem, which involves factoring and finding possible rational roots. Another method is by using the quartic formula, which can be more complex but can find all solutions, including irrational and complex roots.
Fourth degree equations play an important role in many areas of mathematics and physics, including in the study of vibrations, oscillations, and wave phenomena. They are also used in solving optimization problems and in the development of computer algorithms.
No, a fourth degree equation can have at most four distinct solutions. This is because a fourth degree equation can be factored into two quadratic equations, each of which can have at most two solutions. Therefore, the total number of solutions is limited to four.
Fourth degree equations can be used to model a wide range of real-world phenomena, such as the motion of a pendulum, the vibration of a guitar string, and the trajectory of a projectile. They are also used in engineering and economics to solve optimization problems and in computer graphics to create smooth curves and surfaces.