mcastillo356
Gold Member
- 634
- 342
- Homework Statement
- The exercise is about, concerned with the catenary. But, algebraicaly solved, some sketch was missing.
- Relevant Equations
- ##y=y_0\,cosh{\cfrac{x}{y_0}}##
##y'=sinh{\cfrac{x}{y_0}}##
Statement
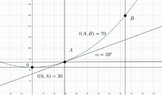
The vertical component of the force exerted on the balloon in the figure is ##500\,N##. The ##AB## cable has a length of ##70\,m## and a weight per unit length of ##q=5\,N/m##. Calculate the horizontal component of the force exerted on the balloon, and the height of the globe, assuming the system is in equilibrium.
Algebraic solution
As we know there are two points, ##A## and ##B##, we use the following notation for the stresses: ##T_A## and ##T_B##, and ##T_{A_x}##, ##T_{A_y}##,##T_{B_x}##,##T_{B_y}## for the horizontal and vertical components. We will also use the concept of length of arch. We will assume that the arch ##AB## belongs to a catenary with the following notation: ##y=y_0\,cosh{\cfrac{x}{y_0}}## respect a cartesian coordinate system with no origin at ##A## nor ##B##.
It is known that at any point of the cable, the vertical component of the stress is directly proportional to the length of the arch, ##s##, being the proportionality constant the weight of the cable per length unit, ##q##. Also, the horizontal component is constant.
So, ##T_{B_y}=q\,s_B\Longleftrightarrow{500=5\,s_B}\Longleftrightarrow{s_B=100\,m}##
Thus, ##s_A=100-70=30\,m##
$$s_A=\displaystyle\int_0^{x_A}\,\sqrt{1+[y'(x)]^2}\,dx=y_0\,sinh{\cfrac{x_A}{y_0}}\Longleftrightarrow{30=y_0\,sinh{\cfrac{x_A}{y_0}}}=y_0\cdot{y'(x_A)}=y_0\,\tan{20^o}\Longrightarrow{y_0=\cfrac{30}{\tan{20^o}}}$$
Thus, respect to the horizontal component of the force made to the globe,
$$T_{B_x}=T_0=q\,y_0=5\cdot{\cfrac{30}{\tan{20^o}}}=412.12\,N$$
Also,
$$\cosh{\cfrac{x_A}{y_0}}=\sqrt{1+sinh^2{\cfrac{x_A}{y_0}}}=\sqrt{1+\tan^2{20^o}}\Longrightarrow{ y_A=y_0\,\cosh{\cfrac{x_A}{y_0}}=y_0\,\sqrt{1+\tan^2{20^o}}=30\sqrt{1+\cot^2{20^o}}}$$
On the other side
$$s_B=\displaystyle\int_0^{x_B}\,\sqrt{1+[y'(x)]^2}\,dx=y_0\,\sinh{\cfrac{x_B}{y_0}}\Longleftrightarrow{100=y_0\sinh{\cfrac{x_B}{y_0}}}\Longrightarrow{\sinh{\cfrac{x_B}{y_0}}}=\cfrac{100}{y_0}\Longrightarrow{\cosh{\cfrac{x_B}{y_0}}}=\sqrt{1+\sinh^2{\cfrac{x_B}{y_0}}}=\sqrt{1+\bigg (\cfrac{100}{y_0}\bigg )^2}\Longrightarrow{}$$
$$y_B=y_0\,\sqrt{1+\bigg (\cfrac{100}{y_0}\bigg )^2}=30\,\sqrt{\cfrac{100}{9}+\cot^2{20^o}}$$
Knowing the ordinates of both positions, we compute the difference
$$h=y_B-y_A=30\,\sqrt{\cfrac{100}{9}+\cot^2{20^o}}-30\,\sqrt{1+\cot^2{20^o}}\Longleftrightarrow{h=41.876\,m}$$
Finally, the calculus that inspired the Geogebra file I've drawn is this:
If ##s_B=100##, ##l(AB)=70##, then
$$s_B\,:=\displaystyle\int_0^{x_B}\sqrt{1+[y'(x)]^2}\,dx=\displaystyle\int_0^{x_A}\sqrt{1+[y'(x)]^2}\,dx+\displaystyle\int_{x_A}^{x_B}\sqrt{1+[y'(x)]^2}\,dx\Longrightarrow{s_B=s_A+l(AB)}\Longrightarrow{s_A=100-70=30}$$
There goes. No preview.
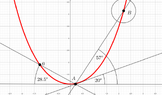

The vertical component of the force exerted on the balloon in the figure is ##500\,N##. The ##AB## cable has a length of ##70\,m## and a weight per unit length of ##q=5\,N/m##. Calculate the horizontal component of the force exerted on the balloon, and the height of the globe, assuming the system is in equilibrium.
Algebraic solution
As we know there are two points, ##A## and ##B##, we use the following notation for the stresses: ##T_A## and ##T_B##, and ##T_{A_x}##, ##T_{A_y}##,##T_{B_x}##,##T_{B_y}## for the horizontal and vertical components. We will also use the concept of length of arch. We will assume that the arch ##AB## belongs to a catenary with the following notation: ##y=y_0\,cosh{\cfrac{x}{y_0}}## respect a cartesian coordinate system with no origin at ##A## nor ##B##.
It is known that at any point of the cable, the vertical component of the stress is directly proportional to the length of the arch, ##s##, being the proportionality constant the weight of the cable per length unit, ##q##. Also, the horizontal component is constant.
So, ##T_{B_y}=q\,s_B\Longleftrightarrow{500=5\,s_B}\Longleftrightarrow{s_B=100\,m}##
Thus, ##s_A=100-70=30\,m##
$$s_A=\displaystyle\int_0^{x_A}\,\sqrt{1+[y'(x)]^2}\,dx=y_0\,sinh{\cfrac{x_A}{y_0}}\Longleftrightarrow{30=y_0\,sinh{\cfrac{x_A}{y_0}}}=y_0\cdot{y'(x_A)}=y_0\,\tan{20^o}\Longrightarrow{y_0=\cfrac{30}{\tan{20^o}}}$$
Thus, respect to the horizontal component of the force made to the globe,
$$T_{B_x}=T_0=q\,y_0=5\cdot{\cfrac{30}{\tan{20^o}}}=412.12\,N$$
Also,
$$\cosh{\cfrac{x_A}{y_0}}=\sqrt{1+sinh^2{\cfrac{x_A}{y_0}}}=\sqrt{1+\tan^2{20^o}}\Longrightarrow{ y_A=y_0\,\cosh{\cfrac{x_A}{y_0}}=y_0\,\sqrt{1+\tan^2{20^o}}=30\sqrt{1+\cot^2{20^o}}}$$
On the other side
$$s_B=\displaystyle\int_0^{x_B}\,\sqrt{1+[y'(x)]^2}\,dx=y_0\,\sinh{\cfrac{x_B}{y_0}}\Longleftrightarrow{100=y_0\sinh{\cfrac{x_B}{y_0}}}\Longrightarrow{\sinh{\cfrac{x_B}{y_0}}}=\cfrac{100}{y_0}\Longrightarrow{\cosh{\cfrac{x_B}{y_0}}}=\sqrt{1+\sinh^2{\cfrac{x_B}{y_0}}}=\sqrt{1+\bigg (\cfrac{100}{y_0}\bigg )^2}\Longrightarrow{}$$
$$y_B=y_0\,\sqrt{1+\bigg (\cfrac{100}{y_0}\bigg )^2}=30\,\sqrt{\cfrac{100}{9}+\cot^2{20^o}}$$
Knowing the ordinates of both positions, we compute the difference
$$h=y_B-y_A=30\,\sqrt{\cfrac{100}{9}+\cot^2{20^o}}-30\,\sqrt{1+\cot^2{20^o}}\Longleftrightarrow{h=41.876\,m}$$
Finally, the calculus that inspired the Geogebra file I've drawn is this:
If ##s_B=100##, ##l(AB)=70##, then
$$s_B\,:=\displaystyle\int_0^{x_B}\sqrt{1+[y'(x)]^2}\,dx=\displaystyle\int_0^{x_A}\sqrt{1+[y'(x)]^2}\,dx+\displaystyle\int_{x_A}^{x_B}\sqrt{1+[y'(x)]^2}\,dx\Longrightarrow{s_B=s_A+l(AB)}\Longrightarrow{s_A=100-70=30}$$
There goes. No preview.


Last edited: