I want to smooth this function plot

[adan]

Hi,
I have the following function, which is computed by: (x+n)/(x+y+n+m),
where x, y are real numbers
n, m are natural numbers

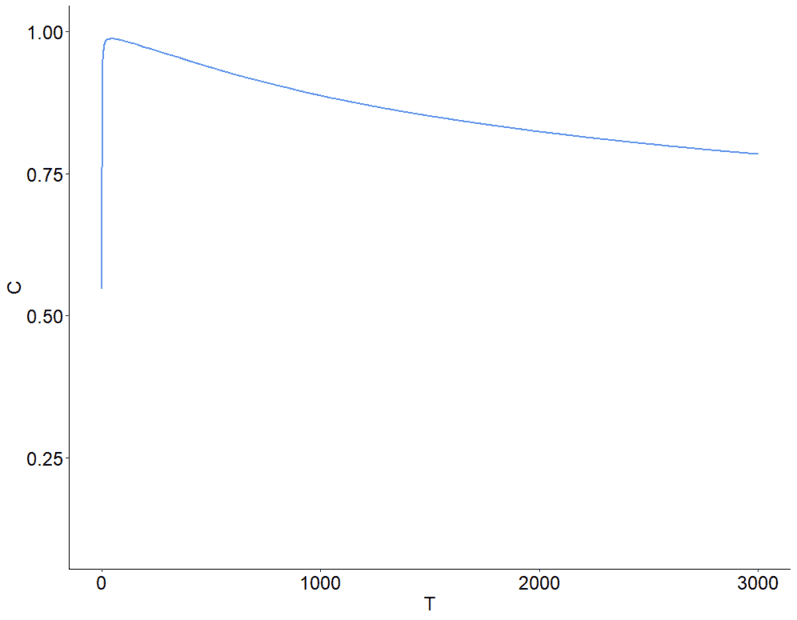
What techniques I can use to smooth the function preventing it to jump up or down at an early stage.

I would appreciate your suggestion.
Thanks

 

[Office_Shredder]

I'm confused, your axis on the bottom is labeled as T, what does that have to do with your function?

I kind of assumed x and y were both inputs into your function, so I'm confused how you graphed it like this in general.

 

[adan]

I'm confused, your axis on the bottom is labeled as T, what does that have to do with your function?

I kind of assumed x and y were both inputs into your function, so I'm confused how you graphed it like this in general.

Thank you. T represents the time. It seems that n increases quickly in the early timesteps. I am still thinking of ways to use T in the formula.

 

[jbriggs444]

Thank you. T represents the time. It seems that n increases quickly in the early timesteps. I am still thinking of ways to use T in the formula.

You have still not told us what it is that you have graphed.

 

[Mark44]

The graph in post #1 makes no sense given your formula. The labels on the graph are C and T, but the formula appears to be a function of x and y, as well as m and n.

Disregarding the m and n terms for the moment, if you have $f(x, y) = \frac x {x + y}$, the graph will be a surface in three dimensions, with a discontinuity along the line y = -x.

 

[fresh_42]

The formula, as well as the graph, are already smooth within their domain.

 

[adan]

Thank you. Yes, I just want to slow down the jump at the beginning.

 

[berkeman]

Thank you. Yes, I just want to slow down the jump at the beginning.

So please provide the following functions, as you've already been asked:

x(T)
n(T)
y(T)
m(T)

 

[adan]

So please provide the following functions, as you've already been asked:

x(T)
n(T)
y(T)
m(T)

x,n,y,m are variables that are changing over time

 

[berkeman]

x,n,y,m are variables

You have a plot with them! Show us the funtion that you used to generate the plot please.

 

[adan]

You have a plot with them! Show us the funtion that you used to generate the plot please.

I construct the function but not fully sure if it is the best way to put all the variables together. I am building a simulation and trying to model human decisions but my model is very simple. The function is above with the question. x and y represent positive and negative personal experiences. n and m represent positive and negative opinions on social media. I assume the combination of all variables specifies the probability of consumption. Because at the beginning of the simulation, social media has 0 opinions, at step 1, multiple opinions are posted.

 

[fresh_42]

You have plotted a function $F\, : \, \mathbb{R}^+\longrightarrow [0,1]$ which means for any value $T\in \mathbb{R}^+$ you plotted a point $(T,F(T)).$ Our question is: What is $F$? It depends only on $T$, so how do we get from $\dfrac{x+n}{x+n+y+m}$ to $F(T)$?

 

[adan]

You have plotted a function $F\, : \, \mathbb{R}^+\longrightarrow [0,1]$ which means for any value $T\in \mathbb{R}^+$ you plotted a point $(T,F(T)).$ Our question is: What is $F$? It depends only on $T$, so how do we get from $\dfrac{x+n}{x+n+y+m}$ to $F(T)$?

F depends on all x,y,n,m, and T also.

 

[berkeman]

Sigh. Your obfuscations will get you nowhere...

Whatever. If you don't like the first point, then just don't plot it. How's that for a solution?

 

[adan]

Sigh. Your obfuscations will get you nowhere...

Whatever. If you don't like the first point, then just don't plot it. How's that for a solution?

Ok, thank you. I will look into your suggestion.

 

[jim mcnamara]

Okay. Will close the thread, we seem to have the kind of answer that the OP wanted.