adan
- 13
- 3
Hi,
I have the following function, which is computed by: (x+n)/(x+y+n+m),
where x, y are real numbers
n, m are natural numbers
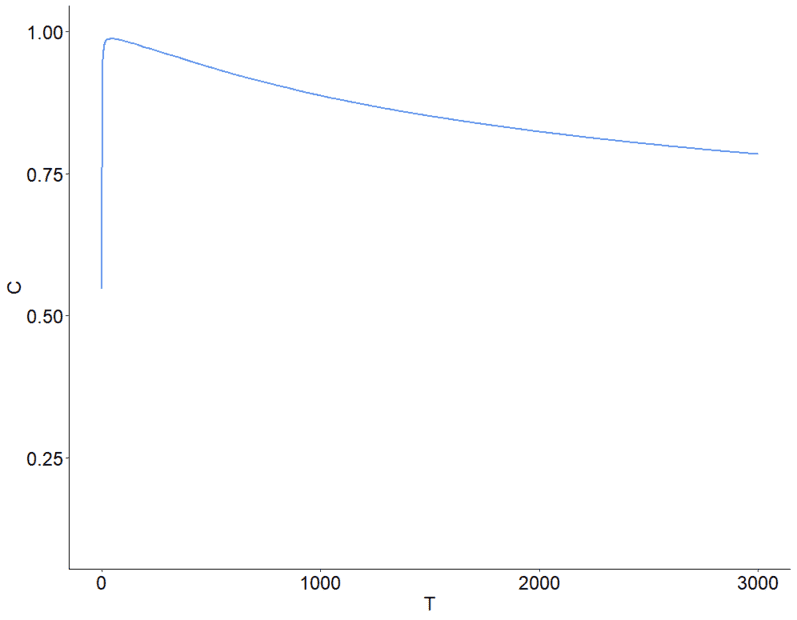
What techniques I can use to smooth the function preventing it to jump up or down at an early stage.
I would appreciate your suggestion.
Thanks
I have the following function, which is computed by: (x+n)/(x+y+n+m),
where x, y are real numbers
n, m are natural numbers
What techniques I can use to smooth the function preventing it to jump up or down at an early stage.
I would appreciate your suggestion.
Thanks