Ideal gas law- Find the pressure

[Woopa]

Homework Statement

A container of an ideal gas that is isolated from its surroundings is divided into two parts. One part has double the volume of the other. The pressure in each part is p and the temperature is the same. The partition is removed. What is the pressure in the container now?

Relevant Equations

PV=nRT

Question:

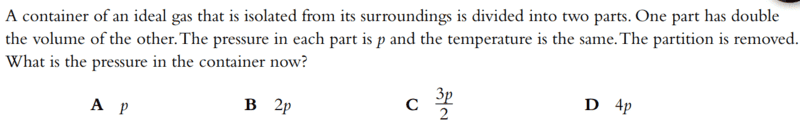
Answer:

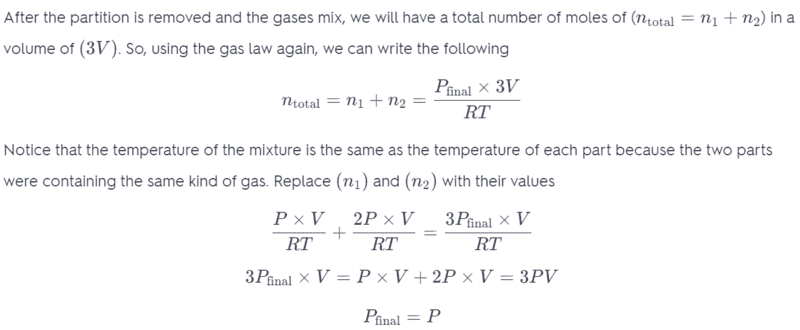
In the third last line of working, I do not understand why the pressure variable is changing? Shouldn't pressure remain constant and only the Volume change?

 

[BvU]

In the third last line of working, I do not understand why the pressure variable is changing? Shouldn't pressure remain constant and only the Volume change?

Where do you see anything changing ? Strictly speaking $p_{\rm\, final}$ is unknown and to be determined.
Then the outcome is $p_{\rm \, final} = p$

Comment: they use capital $P$ in the solution, which is undesirable: once lower case $p$ , always lower case $p$

$\$

 

[Lnewqban]

The 2 and 3 numbers are for V rather than for p.

 

[Woopa]

The 2 and 3 numbers are for V rather than for p.

Do you mean it is a typo/ error in the worked solution?

 

[Lnewqban]

V + 2V = 3V

 

[Woopa]

V + 2V = 3V

Ah yes that make sense I can see now the numbers are actually for V, the way they've written out the equation has confused me.

However I am still arriving at the final answer P=2P. I must be making a mistake in my algebra. I will post my working in a moment

 

[Woopa]

Where is my mistake?

 

[Lord Jestocost]

$p⋅V/RT+p⋅(2V)/RT=p⋅(V+2V)/RT$

 

[Mister T]

$pV+2pV=p(V+2V)=3pV$

You are saying that it's equal to $6pV$. That's your error.