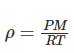Ideal gas law in terms of density

Click For Summary
SUMMARY

The discussion focuses on applying the Ideal Gas Law (PV=nRT) to derive pressure as a function of height using density. The participants explore the integration of the equation -ρg = -PMg/RT = dP/dy, emphasizing the need for understanding integration techniques. The conversation highlights the importance of recognizing n as the number of moles, defined as mass divided by molecular mass. The final goal is to evaluate pressure at a specific height (8812 m) using definite integration.

PREREQUISITES
  • Understanding of the Ideal Gas Law (PV=nRT)
  • Basic knowledge of calculus, specifically integration and differentiation
  • Familiarity with physical concepts of pressure and density
  • Knowledge of constants such as gravitational acceleration (g) and gas constant (R)
NEXT STEPS
  • Learn integration techniques, particularly definite and indefinite integrals
  • Study the relationship between pressure, density, and height in fluid mechanics
  • Explore the application of the Ideal Gas Law in various thermodynamic processes
  • Investigate the significance of molecular mass in gas calculations
USEFUL FOR

Students studying physics or chemistry, particularly those focusing on thermodynamics and fluid mechanics, as well as educators seeking to clarify concepts related to the Ideal Gas Law and integration techniques.

goonking
Messages
434
Reaction score
3

Homework Statement


upload_2015-5-15_2-14-24.png


Homework Equations


PV=nRT

The Attempt at a Solution


not sure if this is the right approach

upload_2015-5-15_2-17-38.png


plugging into -ρg gives us -PMg/RT = dP/dy

now we have to integrate both sides to find P?
 

Attachments

  • upload_2015-5-15_2-19-43.png
    upload_2015-5-15_2-19-43.png
    774 bytes · Views: 484
Physics news on Phys.org
How you can write n as?
 
Raghav Gupta said:
How you can write n as?
n? number of moles?
 
goonking said:
n? number of moles?
Yes
 
n = mass/molecular mass
 
goonking said:

Homework Statement


View attachment 83508

Homework Equations


PV=nRT

The Attempt at a Solution


not sure if this is the right approach

View attachment 83509

plugging into -ρg gives us -PMg/RT = dP/dy

now we have to integrate both sides to find P?
The approach is right. What do you get if you integrate?
 
Raghav Gupta said:
The approach is right. What do you get if you integrate?
well, i have no idea how to integrate that! :(

i only know how to integrate stuff like x2 + 3
 
goonking said:
well, i have no idea how to integrate that! :(

i only know how to integrate stuff like x2 + 3
No, problem.
Do you know differentiation?
 
Raghav Gupta said:
No, problem.
Do you know differentiation?
no, I'm suppose to take that next year :(
 
  • #10
goonking said:
no, I'm suppose to take that next year :(
Oh, okay
Then for the moment remember
$$ \int dx/x = lnx + C $$
Now use this in your problem.
And tell what you are getting.
 
  • #11
Raghav Gupta said:
Oh, okay
Then for the moment remember
$$ \int dx/x = lnx + C $$
Now use this in your problem.
And tell what you are getting.
i'm staring at this and still have no idea what to do, ok, so I know i can take the constants out and put it behind the integral

(-Mg/RT) ∫ P = dP/dy

correct? all the constants are out except P
 
  • #12
Ah, you may also not know the definite integration. I may have to do lot of work here.
$$ \frac{-Mg}{RT}\int_0^{8812} dy = \int_{10^5}^P \frac{dp}{P} $$
At ground height is zero and pressure 105 pascals.
At height 8812 m we have to find pressure. The limits are taken accordingly.
Now I guess you know how to solve further ?
 
  • Like
Likes   Reactions: goonking
  • #13
Raghav Gupta said:
Ah, you may also not know the definite integration. I may have to do lot of work here.
$$ \frac{-Mg}{RT}\int_0^{8812} dy = \int_{10^5}^P \frac{dp}{P} $$
At ground height is zero and pressure 105 pascals.
At height 8812 m we have to find pressure. The limits are taken accordingly.
Now I guess you know how to solve further ?
the left side of the equation should equal -1.095, correct?
 
  • #14
goonking said:
the left side of the equation should equal -1.095, correct?
I must go to school now, i will finish this problem next time.
 
  • #15
goonking said:
the left side of the equation should equal -1.095, correct?
Yes, and what right side evaluates to?
 

Similar threads

Find temperature of a U-shaped Tube
  • · Replies 9 ·
Replies
9
Views
911
Ideal Gas Law and Pressure at 80°C
  • · Replies 2 ·
Replies
2
Views
3K
What would be a real-life example of the ideal gas law?
  • · Replies 3 ·
Replies
3
Views
10K
Incompatibility between ideal gas equations of state
  • · Replies 2 ·
Replies
2
Views
2K
Force acting on the area of the cylinder due to gas
  • · Replies 3 ·
Replies
3
Views
3K
How do I calculate work and heat in a PV diagram for an ideal monoatomic gas?
  • · Replies 11 ·
Replies
11
Views
2K
Spherical gas distributed symmetricaly over space
  • · Replies 3 ·
Replies
3
Views
1K
Calculations using the Ideal Gas Law
  • · Replies 2 ·
Replies
2
Views
2K
How Does the Ideal Gas Law Apply in Multi-Part Physics Problems?
  • · Replies 14 ·
Replies
14
Views
2K
What Happens When Gas Expands at Constant Pressure?
  • · Replies 12 ·
Replies
12
Views
7K