Ideal Transformers and finding the steady state current?

In summary, the conversation discusses the calculation of steady state current in a circuit with a 120V, 60Hz source supplying an ideal load through an ideal 2:1 transformer. The formula used to calculate impedance is Zeq = (1/Z1+ 1/Z2)^-1, where Z1 is 10+j(60*10^-3) and Z2 is 10. The correct Zeq is 5.171+ j0.91. The conversation also touches on the relationship V/Z=I and a thought experiment involving a 60 watt resistive load on the secondary side. It is determined that the load looking from the primary side would be 240 ohms.
  • #1
mikehsiao789
14
0

Homework Statement



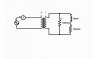
In the circuit shown the 120V, 60Hz source supplies the ideal load shown through an ideal 2:1 transformer. What steady state current would you expect to read on the rms ammeter shown (please find the picture attached)?

Homework Equations


Zeq = (1/Z1+ 1/Z2)^-1
Z1 = 10+j(60*10^-3)
Z2= 10
V/Z=I

The Attempt at a Solution


What I did first was at the right side I combined the impedances and got Zeq as 9.53+j1.5068. Then I transformed it over to the primary side by multiplying but it's ratio, which is two. I get 19.027 + j3.013. Then I use the relationship V/Z=I to obtain 120/(19.027+j3.013) = 6.15-j0.97 or 6.229A with a phase angle of -9 degrees. However I am not sure if I got the right answer (there are no solutions to this...) Help!
 

Attachments

  • abcccccc.png
    abcccccc.png
    59.7 KB · Views: 591
Physics news on Phys.org
  • #2
▸ What formula should you use when calculating the impedance of a 10mH inductance at 60Hz??

Here's a thought experiment...

▸ Suppose you have a 60 watt resistive load on the secondary side (60V & 1A, so that implies the load is 60Ω). A 60 watt equivalent load if located on the primary side where the voltage is 120V would require a current of how much? This implies the equivalent load on the primary side must therefore be how many ohms?
 
  • #3
I realized I made a mistake, the impedance should we Z1= 10 + j*60*2pi*10^-3 and Z2 remains the same... which would give me a Zeq of: 5.171+ j0.91.

Umm, if I had a 60 Watt resistive load on the secondary side, with 120V, the current on the primary side must be 0.5A, which means the load would be 240 Ohms?
Thanks so much for your help!
 
  • #4
mikehsiao789 said:
I realized I made a mistake, the impedance should we Z1= 10 + j*60*2pi*10^-3 and Z2 remains the same...
Right.
Umm, if I had a 60 Watt resistive load on the secondary side, with 120V, the current on the primary side must be 0.5A, which means the load would be 240 Ohms?
Thanks so much for your help!
Yes, load looking from primary is 60*22 = 240 ohms.
 
  • #5
  1. So,with a little thought experiment, you can remind yourself that the transformer transforms impedances according to n2.
 

1. What is an ideal transformer?

An ideal transformer is a theoretical device that is used in electrical circuits to step up or step down the voltage of an alternating current (AC). It consists of two coils of wire, known as the primary and secondary coils, wrapped around a common iron core. The primary coil is connected to the source of AC voltage, while the secondary coil is connected to the load. An ideal transformer has no losses and can transfer power from the primary to the secondary coil without any energy loss.

2. How do you calculate the turns ratio of an ideal transformer?

The turns ratio of an ideal transformer is equal to the ratio of the number of turns in the secondary coil to the number of turns in the primary coil. This can be calculated by dividing the voltage on the secondary coil by the voltage on the primary coil. For example, if the secondary coil has 100 turns and the primary coil has 50 turns, the turns ratio would be 100/50 = 2.

3. What is the steady state current in an ideal transformer?

The steady state current in an ideal transformer is determined by Ohm's law, which states that current is equal to the voltage divided by the resistance. In an ideal transformer, there is no resistance, so the steady state current will be equal to the voltage divided by the impedance of the circuit. This current will remain constant as long as the voltage and impedance do not change.

4. How do you find the steady state current in an ideal transformer?

To find the steady state current in an ideal transformer, you will need to know the turns ratio, the voltage on the primary coil, and the impedance of the circuit. First, calculate the voltage on the secondary coil by multiplying the voltage on the primary coil by the turns ratio. Then, use Ohm's law to calculate the steady state current by dividing the voltage on the secondary coil by the impedance of the circuit.

5. What are some practical applications of ideal transformers?

Ideal transformers are used in a variety of applications, such as power distribution, voltage regulation, and electronic devices. They are commonly used in power grids to step up the voltage for transmission over long distances and then step it down for use in homes and businesses. They are also used in electronic devices to convert AC voltage to DC voltage and to isolate different parts of a circuit.

Similar threads

Engineering Sinusoidal steady state analysis using Laplace transform
    • Engineering and Comp Sci Homework Help
Replies
3
Views
1K
Engineering Alternating current circuit with transformer
    • Engineering and Comp Sci Homework Help
Replies
12
Views
957
Solving Equation to Analyze Steady State Current
    • Introductory Physics Homework Help
Replies
7
Views
1K
Engineering DC Steady State Circuit Analysis: Solving for iL, i, and Vc in a Simple Circuit
    • Engineering and Comp Sci Homework Help
Replies
14
Views
3K
Determining steady state current from phasor current?
    • Engineering and Comp Sci Homework Help
Replies
1
Views
3K
MHB Find Steady States for Equations: u, v and Get Help with Steady State Question
    • Calculus
Replies
1
Views
589
Engineering AC Circuit Phasors: Find I1, I2, I3
    • Engineering and Comp Sci Homework Help
Replies
26
Views
2K
Engineering Basic AC Circuit Question on Equivalent Impedance
    • Engineering and Comp Sci Homework Help
Replies
4
Views
3K
Isentropic Efficiency and Entropy Production Rate of Turbine
    • Engineering and Comp Sci Homework Help
Replies
5
Views
3K
Finding Steady State Amplitude of Voltage Across Load Resistor
    • Engineering and Comp Sci Homework Help
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top