trytodoit
- 8
- 0
Today, I discussed my friend about two rigid beams impact and assuming no energy loss in the impaction.
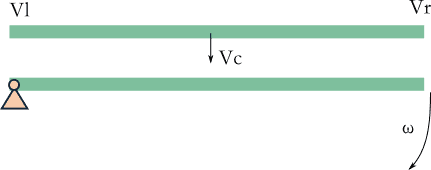
As in the above figure, the upper beam move down with a uniform velocity ##v_c##, and hit a beam with ##0## velocity. After that the above beam will rotate and move away, which can be described by left end velocity ##v_l## and right hand velocity ##v_r##; the lower beam will rotate around the pined point at a angular velocity ##\omega##. Therefore, we have three free variables, but only to equations, one is conservation of angular moment, the other is conservation of energy. Consequently, there are infinite combination of these three variables, which is not intuitive.
For one rigid ball hit the beam, if there is no energy loss in the impaction, there will be only one solution. Why for two beams case, there are infinite number of combinations? If there are infinite combinations, what is the property that determine which combination of the three variable for the impaction?
As in the above figure, the upper beam move down with a uniform velocity ##v_c##, and hit a beam with ##0## velocity. After that the above beam will rotate and move away, which can be described by left end velocity ##v_l## and right hand velocity ##v_r##; the lower beam will rotate around the pined point at a angular velocity ##\omega##. Therefore, we have three free variables, but only to equations, one is conservation of angular moment, the other is conservation of energy. Consequently, there are infinite combination of these three variables, which is not intuitive.
For one rigid ball hit the beam, if there is no energy loss in the impaction, there will be only one solution. Why for two beams case, there are infinite number of combinations? If there are infinite combinations, what is the property that determine which combination of the three variable for the impaction?