Nur Ziadah
- 34
- 3
- TL;DR Summary
- Clarification on the calculation of SKR over turbulence channel.
I have the calculation on secret key rate over the turbulence channel using Python code. The calculation is as below:
Theoretically, the SKR is low in high turbulence (sigma=0.9) and the SKR is high in low turbulence (sigma=0.3). However, after I ran this code, I get the wrong plot:
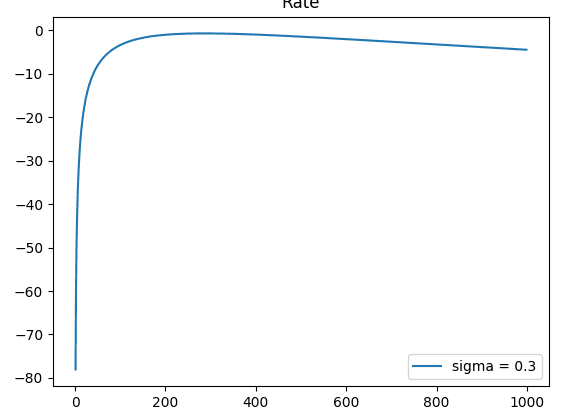
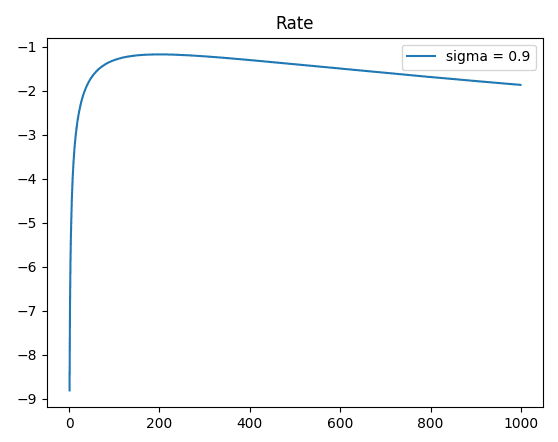
From the graphs, it can be seen at y-axis that the SKR under strong turbulence is higher compared to weak turbulence and vice versa. What is the problem in my calculation? Anyone, please help me. Thank you.
Python:
import numpy as np
import math
import re
import random
import cmath
#import itertools
from math import pi,e,log
import time
#import xlwt
import matplotlib.pyplot as plt
from scipy.interpolate import splinex=np.linspace(0,1,1000)
def log_normal(x,sigma):
y=1/(x*sigma*np.sqrt(2*np.pi))*np.exp(-(np.log(x/0.3)+(1/2*sigma*sigma))**2/(2*sigma*sigma))
return ydef R(x,nd,Y0,ed):
nsys = x*nd
QBER=((1/2*Y0)+(ed*nsys))/(Y0+nsys)
H2=-QBER*np.log2(QBER)-(1-QBER)*np.log2(1-QBER)
out = (Y0+nsys)*(1-(2*H2))
return outdef out(x,nd,Y0,ed,sigma):
term1 = log_normal(x,sigma)
term2 = R(x,nd,Y0,ed)
return term1*term2
hyp = (0.25,1*(10**-5), 0.03,0.9) #nd,Y0,ed,sigmalg = log_normal(x[1:],hyp[3])
r = R(x[1:],hyp[0],hyp[1],hyp[2])
plt.plot(np.log10 ( out(x,hyp[0],hyp[1],hyp[2],0.9) ),label = "sigma = 0.9" )
plt.plot(np.log10 ( out(x,hyp[0],hyp[1],hyp[2],0.3) ) ,label = "sigma = 0.3")
plt.plot(np.log10 ( out(x,hyp[0],hyp[1],hyp[2],0.6) ) ,label = "sigma = 0.6")
plt.title("Rate")
plt.legend()
plt.show()Theoretically, the SKR is low in high turbulence (sigma=0.9) and the SKR is high in low turbulence (sigma=0.3). However, after I ran this code, I get the wrong plot:
From the graphs, it can be seen at y-axis that the SKR under strong turbulence is higher compared to weak turbulence and vice versa. What is the problem in my calculation? Anyone, please help me. Thank you.