Incircles of triangles proving a point it passes through

  • Thread starter Thread starter mxl117
  • Start date Start date
  • Tags Tags
    Point Triangles
AI Thread Summary
In the discussion about proving that the inscribed circle of triangle ABC touches AB at point X, participants emphasize the importance of accurately drawing the diagram to reflect the problem's conditions. The initial diagram was misleading, as the circles inscribed in triangles ACX and BCX should touch at point Y on line CX. To clarify the situation, it's suggested to first draw the incircle of triangle ABC, which helps in correctly positioning point X. Additionally, introducing a third circle that touches the first two and the remaining sides of the triangle can create a symmetric scenario that aids in the proof. The conversation highlights the need for precise visual representation in geometric proofs.
mxl117
Messages
2
Reaction score
0

Homework Statement


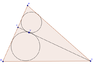
I am given triangle ABC and a point X on the segment AB, one circle is inscribed inside triangle ACX and another inside BCX the two circles touch at point Y which lies on the line CX. show the inscribed circle of ABC touches AB at X


Homework Equations


I suppose you could use the fact the angle bisectors of a triangle is the incenter of the incircle and circumcircle of that triangle.


The Attempt at a Solution


So far i don't have a clue, but i have drawn the diagram. See attached.
If anyone could just get me started i'd be so grateful
 

Attachments

  • incircle problem.png
    incircle problem.png
    6.1 KB · Views: 511
Physics news on Phys.org
welcome to pf!

hi mxl117! welcome to pf! :smile:

ok, your difficulty here is that your diagram really isn't helping …

the place you've put X, those circles should not be touching, so the whole diagram is misleading

start again with a new diagram, and this time draw the incircle of ABC first (that's easy!),

so that you know where X is, and your two small circles really do touch :wink:
 
Thanks :)
ahh sorry i thought i'd done everything the description asked.
Do you have any hints about how to start proving it? because I'm stumped, sorry :(
 
hi mxl117! :smile:

(i haven't solved it, but …)

i'd certainly start by drawing in a third small circle that touches the first two small circles and the remaining pair of sides of the triangle …

you now have a neat symmetric situation, with three small circles touching each other and the three sides :wink:
 
Thread 'Confusion regarding a chemical kinetics problem'

Thread 'Confusion regarding a chemical kinetics problem'

TL;DR Summary: cannot find out error in solution proposed. [![question with rate laws][1]][1] Now the rate law for the reaction (i.e reaction rate) can be written as: $$ R= k[N_2O_5] $$ my main question is, WHAT is this reaction equal to? what I mean here is, whether $$k[N_2O_5]= -d[N_2O_5]/dt$$ or is it $$k[N_2O_5]= -1/2 \frac{d}{dt} [N_2O_5] $$ ? The latter seems to be more apt, as the reaction rate must be -1/2 (disappearance rate of N2O5), which adheres to the stoichiometry of the...
View full post »

Similar threads

MHB Prove Triangle Inequality: AB/MZ + AC/ME + BC/MD ≥ 2t/r
Replies
1
Views
2K
MHB Incircle and circumscribed circle prove :d=√(R(R−2r))
Replies
1
Views
1K
MHB Find maximum area of a triangle
Replies
1
Views
1K
MHB Proving Equality of Angles in an Acute Triangle
Replies
4
Views
1K
I Equation for circle points in 3D
Replies
3
Views
3K
Incircle Trig Problem: Proving a Triangle is Right-Angled | Homework Help
Replies
7
Views
2K
Geometry Problem - Sum of distances
Replies
1
Views
1K
MHB Inscribed circle in the triangle
Replies
2
Views
2K
MHB Proof Quest: Non-Equilateral Triangle Enclosing Point Z
Replies
3
Views
2K
Euclidean and non Euclidean geometries problems
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top