- #1
jtulloss
- 4
- 0
I'm having problems with my initial approach on this problem:
The figure below shows four choices for the direction of a force of magnitude F to be applied to a block on an inclined plane. The directions are either horizontal or vertical. (For choices a and b, the force is not enough to lift the block off the plane.) Rank the choices according to the magnitude of the normal force on the block from the plane, greatest first (use only the symbols > or =, for example c>b>a>d).
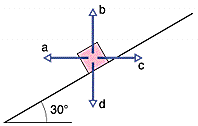
In case the image doesn't work, this is an inclined plane of 30 degrees with a block shown on the plane. The different forces applied are to the block in the +x, -x, +y, and -y directions. I'm supposed to rank the normal force, but I don't even know where to start.
The figure below shows four choices for the direction of a force of magnitude F to be applied to a block on an inclined plane. The directions are either horizontal or vertical. (For choices a and b, the force is not enough to lift the block off the plane.) Rank the choices according to the magnitude of the normal force on the block from the plane, greatest first (use only the symbols > or =, for example c>b>a>d).
In case the image doesn't work, this is an inclined plane of 30 degrees with a block shown on the plane. The different forces applied are to the block in the +x, -x, +y, and -y directions. I'm supposed to rank the normal force, but I don't even know where to start.