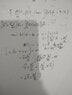Indefinite integral of cross product of 2 function

[agnimusayoti]

Homework Statement

If $\vec{v} (t)$ is a vector function of t, find indefinite integral
$$\int {\left(\vec v \times \frac{d^2 \vec v}{dt^2} dt\right)}$$

Relevant Equations

Idk.

I've tried with this work in attachment. i&m not sure of my answer is correct.

 

[STEMucator]

The problem statement is not given properly. Can you provide us proper details? If you are computing:

$$\int v \frac{d^2v}{dt^2} dt$$​

You mentioned $dv = b(t) dt$, and then computed $v$:

$$v = \frac{dv}{dt}$$​

You know this is inherently not correct, unless the function is specifically $v(t) = e^t$. Don't forget about generality when writing math proofs, or computing such things.

 

[haruspex]

The problem statement is not given properly. Can you provide us proper details? If you are computing:

$$\int v \frac{d^2v}{dt^2} dt$$​

The thread title says cross product.

 

[STEMucator]

Integrate all the remaining terms, and you get a sum of antiderivatives that subtract from the other terms.

I still dislike how we use X for multiplication, and cross product every time I see it, sorry for the confusion.

 

[haruspex]

@agnimusayoti , I think you confused everyone with your unfortunate choice of notation, using v (no arrow) for $\frac{d\vec v}{dt}$ and u for $\vec v$.
Where your algebra goes wrong is in handling $\int \frac{d\vec v}{dt}\times d\vec v$. The correct result becomes obvious if you write it as $\int \frac{d\vec v}{dt}\times \frac{d\vec v}{dt}dt$