Induced current due to a Solenoid

[zorro]

Homework Statement

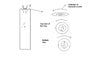
Two metallic rings A and B, identical in shape and size but of different resistivities Pa and Pb are kept of the top of two identical vertical solenoids. When current I is switched on in both the solenoids in an identical manner, the rings A and B jump to heights ha and hb resp, with ha > hb. What are the possible relations between their resistivities and their masses ma and mb?

The Attempt at a Solution

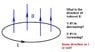
Let us assume that the current in the two solenoids is towards right (as seen from a side) and anticlockwise as seen from the top.
The anticlockwise flow of current at the top creates a north pole there. The magnetic field through the solenoid is directed outwards which induces a clockwise current in the ring. As seen from the bottom, the flow of current in the ring creates a south pole.

The north pole of the solenoid and the south pole of the ring attract each other. Why will the ring jump?

 

[hikaru1221]

Lenz law Hint: B-field is weaker when staying farther from the solenoid.
Besides, your analysis is not correct It's actually the north poles of both face each other. This concurs with Lenz law.

 

[zorro]

See the figure.

 

[hikaru1221]

The direction of induced current is not correct
Tell me the reason why you think it should be in your way.

 

[zorro]

The direction of induced electric field is given by right hand thumb rule. So current flow is in that direction.

 

[hikaru1221]

The direction of induced electric field is given by right hand thumb rule.

See picture.

 

[zorro]

Ah, I never knew that there will be a difference between the increasing and decreasing currents.

In case 1, the induced current is in the same direction of I
In case 2, it is opposite to that of I.

 

[hikaru1221]

Now apply back to your problem

 

[zorro]

Lesser resistivity ring will get greater impulse.
So Pa<Pb and ma><=mb (can take any values - such that ha is always greater than hb). Is it fine?

 

[hikaru1221]

Not really. We have to do some math here.
_ The solenoids will give rise to the same induced emf e = IR.
_ We have the magnetic force on each ring F = kI, where k depends on the B-field of the solenoid and the geometry of the ring and thus is the same for the 2 rings.
_ Therefore: F = ke/R. That means, the impulse given to the ring X ~ 1/R.
_ We have: X = mv, where v is the initial speed. Now assume that the ring will go farther from the solenoid such that it will no longer be affected by B-field of solenoid. Then we have: h = v²/2g.
_ Therefore: 1/mR ~ sqrt(h).
That means: ma*Pa < mb*Pb. Think about it. Even if Pa>Pb, if ma <<<<<<<< mb (ma is very small), then you can lift ring ma more easily than ring mb

 

[zorro]

_ The solenoids will give rise to the same induced emf e = IR.

How did you get that expression?

 

[hikaru1221]

Agree that induced emf inside each ring must be the same?
Apply Ohm's law: e = IR

 

[zorro]

Induced e.m.f using Ohm's law?? You took 'I' (given in question) as the current flowing in the solenoid or the induced current?

 

[hikaru1221]

No, I used Ohm's law to deduce the relation between I and e.
Induced emf is deduced by B-field, geometries of the solenoid and the ring, blah blah blah, but I don't care about that arduous process. The only thing I care is that induced emf is the same. And after I obtain induced emf, I turn my attention to the induced current inside the ring, by Ohm's law: e = IR

 

[zorro]

You denoted 'I' as the induced current. I was confused there. In the question 'I' is the maximum current passing through the solenoid (which builds up from 0)

 

[hikaru1221]

Oops, sorry, I didn't notice that

 

[zorro]

Then I understood everything. Thanks!