- #1
PhiowPhi
- 203
- 8
Assume we have the following copper slab, with volume ##V##, and introduced a magnetic field covering a small area of it like so:
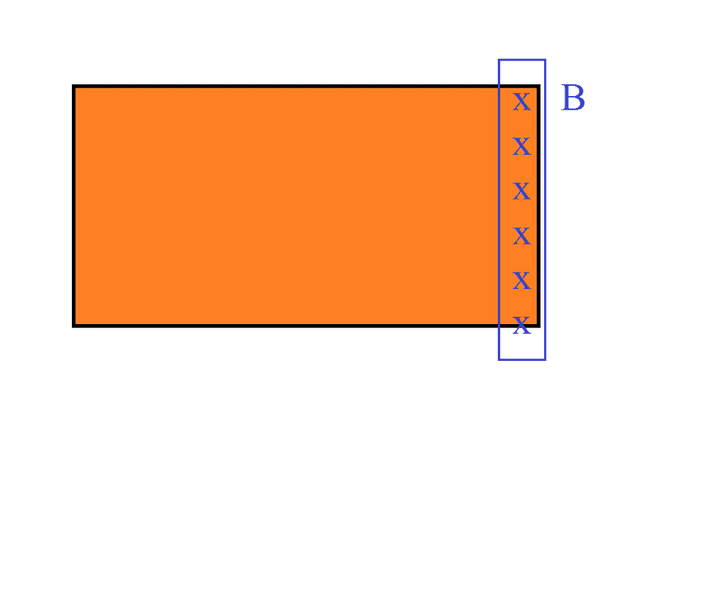
There is change in magnetic flux(##\phi##) due to the magnetic field increasing/decreasing, and via Faraday & Len'z law of electromagnetism, there is an induced EMF(##- \epsilon ##) to oppose that change, and with the conductor's resistance(##r##) an induced current(##I##).
One thing that I'm struggling with, is knowing/understating where the induced EMF is bound to? Is the induced EMF all around the conductor like so:
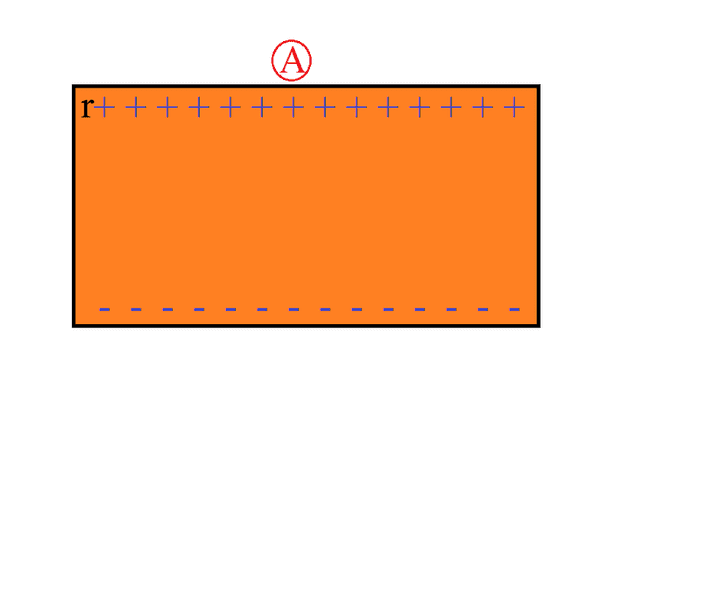
Where if I placed a volt-meter anywhere on the top part (A) and the bottom part, the voltage would be the same any point there?
Or , is the induced EMF limited to the area the magnetic field interact's with like so:
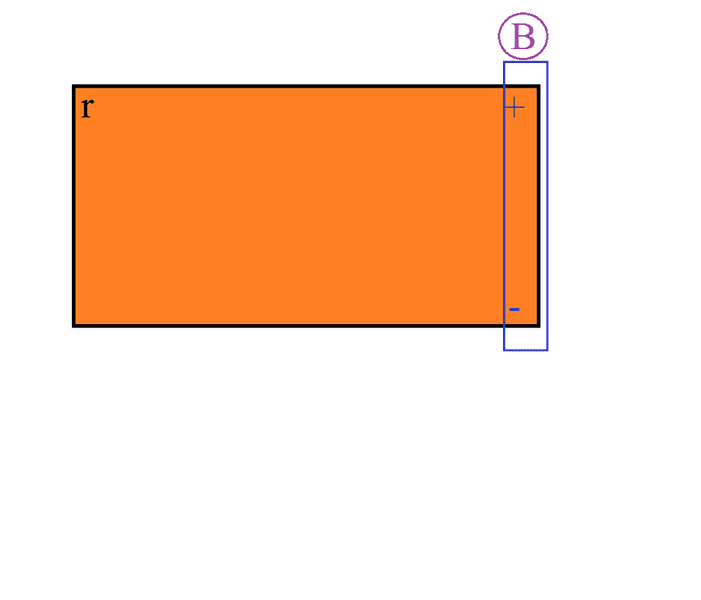
The blue rectangle represents the magnetic field, and r, the resistance of the whole slab.
Likewise, will induced current be focused to that area the magnetic field interacts with, or the entire slab?
One thing I'd like to add, if we introduced and exterior Voltage source to the slab, with the induced EMF, would it be in series?
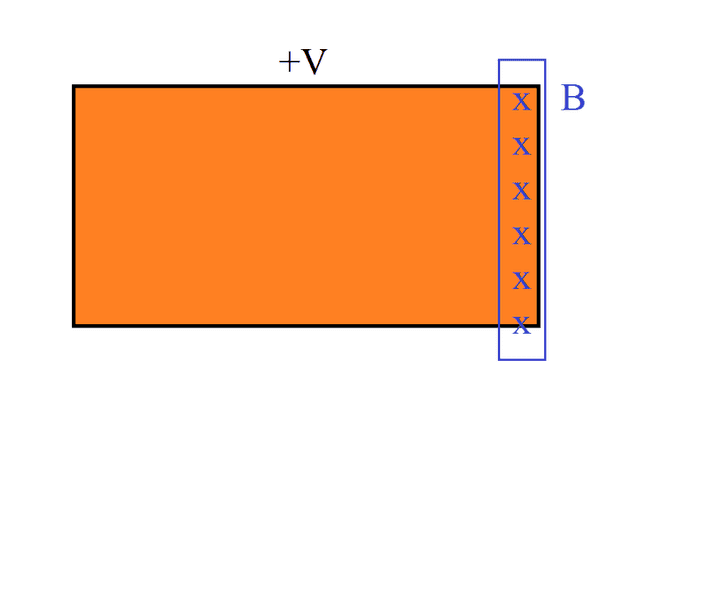
The total voltage if they we're in a circuit, and they are connected to one another the net-voltage in the circuit would be:
##V_n## = ##V## - ##\epsilon## ?
There is change in magnetic flux(##\phi##) due to the magnetic field increasing/decreasing, and via Faraday & Len'z law of electromagnetism, there is an induced EMF(##- \epsilon ##) to oppose that change, and with the conductor's resistance(##r##) an induced current(##I##).
One thing that I'm struggling with, is knowing/understating where the induced EMF is bound to? Is the induced EMF all around the conductor like so:
Where if I placed a volt-meter anywhere on the top part (A) and the bottom part, the voltage would be the same any point there?
Or , is the induced EMF limited to the area the magnetic field interact's with like so:
The blue rectangle represents the magnetic field, and r, the resistance of the whole slab.
Likewise, will induced current be focused to that area the magnetic field interacts with, or the entire slab?
One thing I'd like to add, if we introduced and exterior Voltage source to the slab, with the induced EMF, would it be in series?
The total voltage if they we're in a circuit, and they are connected to one another the net-voltage in the circuit would be:
##V_n## = ##V## - ##\epsilon## ?