- #1
Marcin H
- 306
- 6
I am trying to understand how to derive equations for the inductance of an x-conductor line. Any number really. But I want to understand the proof for a two-conductor line first. So to start any of these proofs you first need the equation for the per unit length inductance:
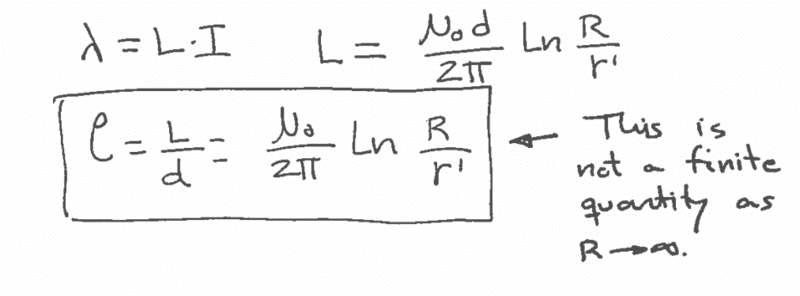
I know R is the distance between the wire and the return path, but I am confused by what r' is in that formula. I know that r' = e^(1/4)*r, where r is the radius of the wire we are looking at. But what does that term in front of r do? What do we call r' or how do we think about it physically? Then we get into the proof itself. Here it is from my notes:
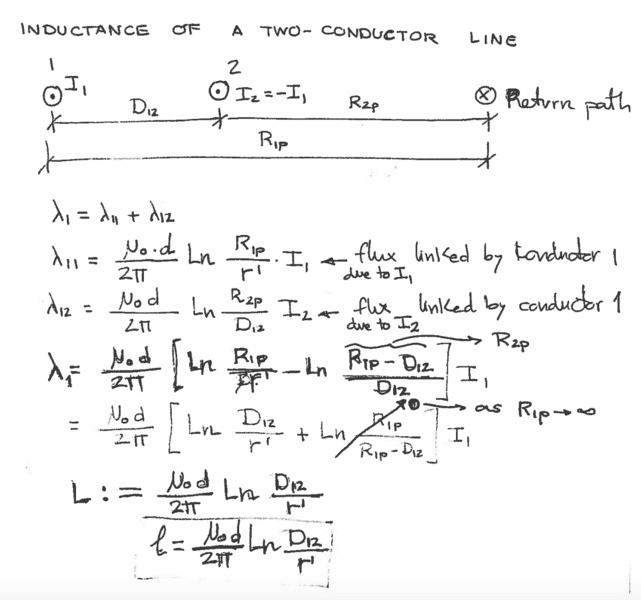
I can follow this for the most part by applying the first equation, but the thing I don't understand at all is where the denominator is coming from in the Ln part of each equation. Why is the denominator for λ_11 r'? and why is the denominator D_12 for the λ_12? This brings me back to my first question of what is r' and how does it change depending on what wire you are looking at. r' is where I get really confused. (Circled in red below)
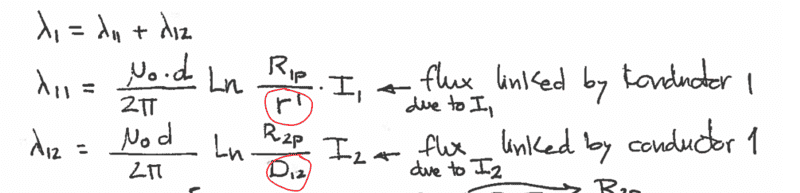
I know R is the distance between the wire and the return path, but I am confused by what r' is in that formula. I know that r' = e^(1/4)*r, where r is the radius of the wire we are looking at. But what does that term in front of r do? What do we call r' or how do we think about it physically? Then we get into the proof itself. Here it is from my notes:
I can follow this for the most part by applying the first equation, but the thing I don't understand at all is where the denominator is coming from in the Ln part of each equation. Why is the denominator for λ_11 r'? and why is the denominator D_12 for the λ_12? This brings me back to my first question of what is r' and how does it change depending on what wire you are looking at. r' is where I get really confused. (Circled in red below)
