Inelastic Collision: Finding Initial Angle

[barryj]

Homework Statement

[/B]
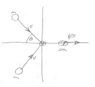
After a completely inelastic collision between two objects of equal mass, each having an initial speed of v, the two move off together with a speed of v/3. What is the angle between their initial directions.

Homework Equations

Conservation of momentum in both x and y directions.

The Attempt at a Solution

See the attached diagram.
Are my equations correct? if so how are they solved.
When plotted they do not cross.

[/B]

 

[kuruman]

If I understand your drawing correctly, the masses move in different direction after the collision. The problem clearly states that "the two move off together". You need to reconsider your approach.

 

[barryj]

Kuruman, No, after the collision, the masses are together and move in the North East direction. about 135 deg
Initially, one mass moves from left to right at 90 deg, the other moves in a 135 deg direction.. Both together move in the direction of V/3.
Let me know if this is unclear

 

[SammyS]

Kuruman, No, after the collision, the masses are together and move in the North East direction. about 135 deg
Initially, one mass moves from left to right at 90 deg, the other moves in a 135 deg direction.. Both together move in the direction of V/3.
Let me know if this is unclear

You don't know the initial or final angles .

There is a much more convenient way to orient the velocity vectors relative to the coordinate axes.

 

[barryj]

I am trying to find the initial angle.

Better way to orient the velocity axis?

 

[kuruman]

OK, I see. If momentum is conserved, you have $\vec p_1+\vec p_2=\vec P$, which can be rewritten as $\vec p_1+\vec p_2+(-\vec P)=0$. You have three vectors, the sum of which is zero. If you draw the usual vector addition diagram, you get a closed triangle. What more can you say about that triangle? How is the traingle related to the drawing you are trying to make?

 

[barryj]

Actually, it seems my equations are correct. My diagram is a bit misleading. Solving the equations by squaring both sides and adding them gives me cos theta = -.777 and theta is 140 degrees.

 

[kuruman]

... theta is 140 degrees.

It's the answer I got using the law of cosines, which is the direction I tried to steer you in.

 

[haruspex]

Actually, it seems my equations are correct. My diagram is a bit misleading. Solving the equations by squaring both sides and adding them gives me cos theta = -.777 and theta is 140 degrees.

It is much simpler to consider the component of the initial velocities that is parallel to the final velocity.

 

[RPinPA]

Now that you've solved the problem, I'll add my comment which I was afraid was too much of a hint, and then show how much simpler the math becomes.

Symmetries often make problems in physics easier. You chose the x-axis to be the direction of one of the initial objects, but a more convenient choice would have been, as @haruspex said, to choose the final momentum as the x-axis. That eliminates the need for the angle $\phi$.

But what is that direction? By a symmetry argument, it has to be exactly halfway between the two identical velocity vectors. It can't be more toward one vector than the other, because there is nothing to distinguish those two directions. If you thought it was 10 degrees above the halfway point, why not 10 degrees below?

You can also prove that to yourself by doing the geometry for the vector addition, say by the parallelogram method.

Once you choose that halfway point as an x-axis, you realize that each original vector makes an angle of $\theta/2$ with the x-axis, the y-components of the original vectors cancel out, and the sum of the original x components of momentum is $2mv \cos(\theta/2) = 2m \cdot v/3$ so $\cos(\theta/2) = 1/3$.

 

[barryj]

It seems to me that you don't know the initial angle theta, or the final angle phi. I did put one of the initial vectors on the x-axis but then it seems to me that you have to solve for both theta and phi. If you ch.oose the final vector on the x axis, then both of the initial axis would be off the x axis. I will continueto think on this.

 

[jbriggs444]

If you ch.oose the final vector on the x axis, then both of the initial axis would be off the x axis. I will continueto think on this.

This is the attractive approach. If you make a diagram, it should be clear that both initial vectors are above and below the x-axis by the same angle. That angle should be easy to determine.

 

[barryj]

I should have used a diagram as follows.

 

[RPinPA]

It seems to me that you don't know the initial angle theta, or the final angle phi.

But you do know by symmetry what $\phi$ has to be in terms of $\theta$. As I said, draw a picture of the vector addition of two equal vectors. It doesn't matter what their length is or what the angle between them is, so long as it's nonzero. What direction is the resultant? You can KNOW this from the picture and a little reasoning.

It's important to realize that there wasn't one right answer here. Your approach was perfectly valid and led to solvable equations. It's just that those of us used to arguments by symmetry perceived a shortcut, an easier but equally valid solution.

It's also kind of interesting that in your equations, $\phi$ turned out to be irrelevant. You could eliminate it even without making any assumptions about symmetry. So that tells you that the magnitude of the final velocity is all you really needed, not its direction.

I had to think about that a minute but it does make sense to me. If I give you two vectors of length $v_1$ and $v_2$ and tell you their resultant has magnitude $v_1 + v_2$, you know they were pointing in the same direction, $\theta = 0$. If the magnitude is $|v_1 - v_2|$ I know they were in opposite directions, $\theta = 180$. And anywhere in between those extremes I can tell you $\theta$ from the magnitude. As somebody said, it's the Law of Cosines underneath that calculation.

 

[barryj]

Actually, if you look at my revised diagram, there is really only one angle to be found.
The equation becomes... 2mvcos(theta) = 2m(v/3) giving theta = cos^-1(2/6) and theta being 70 degrees.
The better diagram makes the problem trivial, yes?

I need to learn Latex.

 

[RPinPA]

Actually, if you look at my revised diagram, there is really only one angle to be found.
The equation becomes... 2mvcos(theta) = 2m(v/3) giving theta = cos^-1(2/6) and theta being 70 degrees.
The better diagram makes the problem trivial, yes?

Yes, but the better diagram is using the symmetry assumption. Which is correct of course, so the diagram is correct.

 

[neilparker62]

Thanks for this question and subsequent thread - I learned a lot especially in respect of the symmetry considerations.

Alternate solution based on the symmetry diagram and energy considerations:
$$sin^2(θ/2)=8/9$$
from which:
$$cos(θ)=1 - 2\times8/9=-7/9$$

 

[barryj]

Where did you get the cos theta = -7/9

 

[neilparker62]

Where did you get the cos theta = -7/9

From the identity:

$$ cos(θ)=1-2sin^2(θ/2) $$

 

[barryj]

OK, so where did you get.. $sin^2(\theta/2) = 8/9$

 

[neilparker62]

My reasoning may be a little contrived but in essence the symmetry diagram resolved momentum parallel and perpendicular to the line of impact which (in your updated diagram) is along the y-axis. As has been mentioned in post #10 the y-components cancel out which means the energy associated with those components of velocity also disappears. The energy loss is thus: $$ 2\times ½ m (v sin(θ/2) )^2=mv^2sin^2(θ/2) $$ From the information given in the question the energy loss is $8/9 mv^2$ from which I conclude: $$ sin^2(θ/2) = 8/9 $$.

 

[kuruman]

Where did you get the cos theta = -7/9

From momentum conservation
$\vec p_1+\vec p_2=\vec P$
Dot each side with itself
$(\vec p_1+\vec p_2)\cdot(\vec p_1+\vec p_2)=\vec P\cdot \vec P$
Expand
$p_1^2+2\vec p_1\cdot \vec p_2+p_2^2=P^2$
The vector magnitudes are
$p_1=p_2=mv;~P=(2/3)mv$
Substitute back and cancel the mass
$2v^2+2v^2 \cos\theta=(4/9)v^2$
Simplify and solve
$1+ \cos\theta=2/9$
$\cos\theta=-7/9$

 

[SammyS]

Where did you get the cos theta = -7/9

@barryj ,
I assume you were asking this of @neilparker62 , since you posted it within 2 hours of his post which ended as follows

...
from which:$$cos(θ)=1 - 2\times8/9=-7/9$$

As you see, you may get other explanations of how to get that answer in ways which are beyond what you were asking about.

To avoid such a possible source of confusion, it's a good idea to use the " Reply " feature. You can always trim the quoted piece to make it as brief as you like.