Inelastic Collision with a Mass attached to a Rod

[yellowcakepie]

Homework Statement

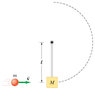
A pendulum consists of a mass M hanging at the bottom end of a massless rod of length l, which has a frictionless pivot at its top end. A mass m, moving as shown in the figure with velocity v impacts M and becomes embedded.

What is the smallest value of v sufficient to cause the pendulum (with embedded mass m) to swing clear over the top of its arc?

Homework Equations

p = mv

The Attempt at a Solution

I know the answer, but I do not understand the logic behind it.

I set mv = (M+m)v_f

then for some reason, I have to use the centripetal acceleration formula a = v_f^2/r which is g = v_f^2/l in our situation.

I find v_f then plug it into the first equation with conservation of momentum to get v = (sqrt(gl)*(M+m))/m.

But this is not the answer. I have to multiply by 2 to get the correct answer. Any explanations?

 

[TSny]

The v_f in your equation mv = (M+m)v_f represents the velocity just after the collision when the two masses are still at the bottom of the circle.

Why set the centripetal acceleration equal to g?

 

[yellowcakepie]

The v_f in your equation mv = (M+m)v_f represents the velocity just after the collision when the two masses are still at the bottom of the circle.

Why set the centripetal acceleration equal to g?

I don't know why. I saw an online solution and copied it.

So if we don't set it to g and just leave it as a, it would be a = (mv/(M+m))^2/l.

al = (mv)^2/(M+m)^2
al(M+m)^2 = (mv)^2
sqrt(al(M+m)^2) = mv

sqrt(al(M+m)^2)/m = v

But a is not given in the problem?

 

[TSny]

My hint would be to say that you don't need to use the concept of acceleration at all.

You used conservation of momentum for the collision, which is good. Can you think of any concept(s) that might be useful for relating the speed just after the collision to the speed at the top? This might be something you studied just previous to your study of momentum.

 

[yellowcakepie]

My hint would be to say that you don't need to use the concept of acceleration at all.

You used conservation of momentum for the collision, which is good. Can you think of any concept(s) that might be useful for relating the speed just after the collision to the speed at the top? This might be something you studied just previous to your study of momentum.

Speed at the top should be 0. So KE = 0 and PE = (m+M)g*2l.

 

[TSny]

Speed at the top should be 0. So KE = 0 and PE = (m+M)g*2l.

OK

 

[yellowcakepie]

Speed at the top should be 0.

OK

PE = (M+m)g*2l
p = mv = (M+m)v_f

(M+m) = mv/v_f (from the momentum equation)
2mvgl/v_f = PE

I don't know where I'm going from here...

 

[TSny]

Step back and think about what's going on with energy once the collision is over. What type(s) of energy does the system have just after the collision? Same question for at the top.

 

[yellowcakepie]

Step back and think about what's going on with energy once the collision is over. What type(s) of energy does the system have just after the collision? Same question for at the top.

It's going to have some kinetic energy at the bottom when they collide.

1/2mv^2 = 1/2(M+m)v_f^2 ? (but this is an inelastic collision)

 

[TSny]

It's going to have some kinetic energy at the bottom when they collide.

1/2mv^2 = 1/2(M+m)v_f^2 ? (but this is an inelastic collision)

Yes, the collision is inelastic. So, the kinetic energy after the collision is not equal to the kinetic energy before the collision. But you've already taken care of the collision using momentum conservation. That is, momentum conservation allows you to find the initial speed, v, of m if you know the final speed v_f just after the collision. So, you can answer the question if you could somehow find v_f. Try to find v_f by considering energy changes in going from just after the collision to the point at the top.