Chalnoth said:
I think you've confused yourself here. This makes no sense. SR doors not have inconsistency problems, and quantum behavior isn't especially important at high velocities (it makes a much bigger difference at low velocities, especially low temperatures).
Anyway, I'll just leave this here:
http://www.preposterousuniverse.com...ion-of-quantum-mechanics-is-probably-correct/
...Carol has a strong opinion on MWI of which is not equally shared in the science community. https://en.wikipedia.org/wiki/Interpretations_of_quantum_mechanics( Tabular comparison)
Well, going back.., we do have have 2 states for instance but the requirement for each state doesn't necessarily be in two separate states each having its own unique Hilbert spaces. It could also be simultaneity in time/observer dependent -- each state could not exist simultaneously at the same time(asumming time is not absolute like QFT -- where it uses both formalism exception of nonrelativistic QM/probabilistic). We would have interval dependent state and since our detectors(time/space affects the outcome/picture of an observer) are not absolute we won't be able to detect a very small time interval of a state. Hence, we are observing weird phenomenon/quantum behavior -- smeared/multiplicity on low scales using direct postulate of the observation. Staying true to SR -- which is compatible to Quantum Field Theory. It has the approximate effect on large/strong gravitational field
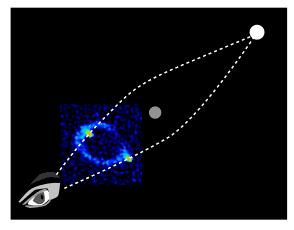
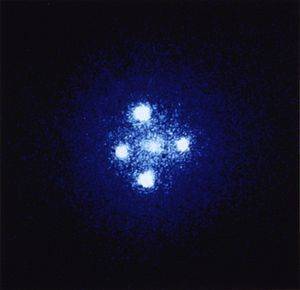
where spacetime is distorted following an image of multiple quasars. At first glance we could easily say it is 5 quasars due to direct detection but in reality it is just 1 when considering SR and lensing -- (which is more to do with formalism and variable treatment on Quantum postulates explained onwards). I always got the doubt the quantum picture is incomplete. This becomes effective solely on how to formulate QFT. We have a choice in making spatial coordinate into parameters(eventually multiple Hilbert spaces), or making time into an observable(satisfies unitarity). I didn't mention any inconsistencies but discontinuity of the formalism. Anyways going back..
If time becomes an operator, In relativistic theories, there is more than one notion of time. We can use the proper time τ of the particle (the time measured by a clock that moves with it) as the time parameter. The coordinate time T (the time measured by a stationary clock in an inertial frame) is then promoted to an operator. In the Heisenberg picture (where the state of the system is fixed, but the operators are functions of time that obey the classical equations of motion), we would have operators Xμ(τ), where X0=T. Relativistic quantum mechanics can indeed be developed along these lines, but it is surprisingly complicated to do so. (The many times are the problem; any monotonic function of τ is just as good a candidate as τ itself for the proper time, and this infinite redundancy of descriptions must be understood and accounted for.) The difference come from the interpretation of the formalisms which affects generalization directions. Take for example, Xμ(τ), why not consider adding some more parameters? Then we would have, for example, Xμ(σ,τ). Classically, this would give us a continuous family of worldlines, what we might call a worldsheet, and so Xμ(σ,τ) -- string picture. The other choice is demoting position to a label or operator. Consider assigning an operator x in space; call these operators ϕ(x). A set of operators like this is called a quantum field. In the Heisenberg picture, the operators are also time dependent: ϕ(x,t)=eiHt/ℏϕ(x,0)e−iHt/ℏ . Thus, both position and (in the Heisenberg picture) time are now labels on operators; neither is itself the eigenvalue of an operator. So, now we have two different approaches to relativistic quantum theory, approaches that might, in principle, yield different results. This, however, is not the case: it turns out that any relativistic quantum physics that can be treated in one formalism can also be treated in the other. Which we use is a matter of convenience and taste. And, quantum field theory, the formalism in which position and time are both labels on operators, is much more convenient and efficient for most problems but could be said the other way around.
Why should assuming absolute time(consequent generalization of multiple unique states-- multiverse/manyworlds anything with many on it lol) or some cutoff and/or idealization treatment on time be the only alternative? BTW I'm not saying macro weirdness/phenomenon(Einstien cross) is on par with quantum weirdness. I'm only stating a critical aspect of spacetime/ problem with taking a strong commitment to direct picture of an observation and how distortions of spacetime could produces weird phenomenon only to be known that is not to be the case..



