Inner working of a linear actuator

AI Thread Summary
The discussion focuses on the working mechanism of a linear actuator, specifically how the force that moves the plunger is generated. It highlights that current applied to the solenoid creates magnetic fields, which are intensified by the plunger's high permeability, resulting in a force that moves the plunger horizontally. Questions arise regarding the relationship between magnetic fields and the direction of force, as well as the energy dynamics involved when the plunger is within the coil. The conversation also touches on the energy required to maintain the magnetic field and the role of dissipation, although it suggests that dissipation is not critical for understanding the force exerted on the plunger. Overall, the interaction of magnetic fields, energy, and force generation in linear actuators is complex and requires further exploration.
geft
Messages
144
Reaction score
0
I need to describe the working mechanism for the following actuator.

gswl6.png


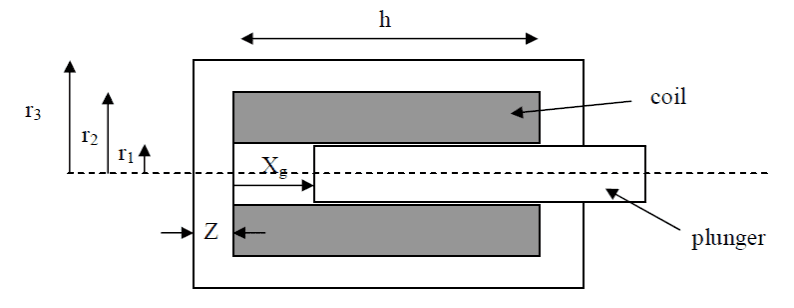
Here's what I've written so far:
Current is applied to the solenoid in order to induce magnetic fields within the actuator in accordance to Ampere’s Law. Since the plunger has high permeability, the magnetic fields produced would be strengthened and confined to the actuator. The fields produce a force which in turn moves the plunger horizontally.

However, I feel that I'm missing something. In particular, how is the force that moves the plunger generated? Is it really due to the magnetic fields? I know of the right hand rule where force points away in the direction of the palm but according to that rule, the force should actually point in the direction perpendicular to the supposed plunger movement. Is it driven by the mmf?
 
Physics news on Phys.org
The simplest way to consider it is through energy: the more "plunger" you have inside the coil, the lower the energy. Force is just the spatial derivative of the energy, so it enters. In fact, in absence of friction, it will just come out the other side and oscillate.

An "Ampere law" version is more complicated, seriously.
 
But where does that energy come from? Since this actuator is driven by current, how does the total electrical energy change with respect to the size of the plunger inside?
 
When putting current through the coil, you need some energy to fight dissipation, and also some energy to create the external magnetic field. The energy of the magnetic field is proportional to the permeability times B^2, integrated to all the volume. When you put the plunger inside the coil, the magnetic field is cheaper to maintain.
 
I see, but why do we need energy to fight dissipation? I thought dissipation is due to energy?
 
Don't worry about dissipation to understand this, even if it is not present, the plunger will feel the force inwards.

In any case, dissipation is due to Joule effect: dissipated power = intensity times voltage drop...
 

Thread 'Is calling fictitious forces "not real" just about terminology?'

Hi there, im studying nanoscience at the university in Basel. Today I looked at the topic of intertial and non-inertial reference frames and the existence of fictitious forces. I understand that you call forces real in physics if they appear in interplay. Meaning that a force is real when there is the "actio" partner to the "reactio" partner. If this condition is not satisfied the force is not real. I also understand that if you specifically look at non-inertial reference frames you can...
View full post »

Thread 'Inclined treadmills and Galilean Invariance'

This has been discussed many times on PF, and will likely come up again, so the video might come handy. Previous threads: https://www.physicsforums.com/threads/is-a-treadmill-incline-just-a-marketing-gimmick.937725/ https://www.physicsforums.com/threads/work-done-running-on-an-inclined-treadmill.927825/ https://www.physicsforums.com/threads/how-do-we-calculate-the-energy-we-used-to-do-something.1052162/
View full post »

Thread 'Derivation of Hamilton's Principle: Questions'

I have recently been really interested in the derivation of Hamiltons Principle. On my research I found that with the term ##m \cdot \frac{d}{dt} (\frac{dr}{dt} \cdot \delta r) = 0## (1) one may derivate ##\delta \int (T - V) dt = 0## (2). The derivation itself I understood quiet good, but what I don't understand is where the equation (1) came from, because in my research it was just given and not derived from anywhere. Does anybody know where (1) comes from or why from it the...
View full post »

Similar threads

How are the connectors on the DC linear actuator utilized in wiring?
Replies
18
Views
2K
Looking for a low-latency force-based actuator - do they exist?
Replies
6
Views
1K
Electromagnet Polarity Switching for Reversed Motion
Replies
7
Views
2K
Linear Actuator Sizing for Angular Force (BMX starting gate)
Replies
9
Views
3K
Locking Mechanism reducing load on locking pin
Replies
2
Views
2K
Non magnetic linear displacement system for moving a Hall Sensor
Replies
11
Views
2K
Calculating acceleration constant for linear actuator
Replies
3
Views
4K
Linear Actuator (Solenoid pushing a cylindrical magnet)
Replies
1
Views
4K
B Non-ferrous solenoid actuator -- Force calculation
Replies
3
Views
2K
I How Do Eddy Current Dampers Work in Space Applications?
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top