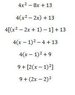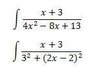Integral Help for Calc II Newbie

[mike01]

Integral Help??Newbie

I apoligize in advance I am a newibe to this forum..

Homework Statement

integral [(x+3)/(4x^2-8x+13)]

Homework Equations

The Attempt at a Solution

I am currently studying CalcII we Just got into evaluating integrals by completing the square in the denometer however I cannot get this one to work out. I attempted to evaluate by completing the square I got 9+(2x-2)^2 but I do cannot get a substitution to the X+3dx, I tried to split it into two with the X/ and the 3/ but again get stumped at the 3/. Just looking for a little guidance that’s all. Thanks in advance for everyone’s help.

 

[Dick]

Your completing the square on (x^2-8x+13) is wrong for a start. Can you show us how you did that?

 

[mike01]

see attached image where did I mess up??

 

[Dick]

see attached image where did I mess up??

Absolutely nothing messed up. You just messed up the initial posting. You left the 4 off of the x^2 in the denominator.

 

[mike01]

now that I have corrected that (sorry) if I factor and complete the square nothing (that I can see) works out good for the "x+3" so I looked at splitting them the "x/" works out and substitutes well then turns into a du/a^2+u^2 or arctan, however I am not sure how to deal with the other with the "3/"?

 

[Dick]

Thanks for the correction. x+3=(1/2)*(2x-2)+4. Is that the sort of relation you are looking for?

 

[mike01]

Dick, where does the 1/2 come from?? does this seem like the logical next step? (See image). Thanks for all your help.

 

[Dick]

You can't argue with x+3=(1/2)*(2x-2)+4, can you? It's just plain true. I worked it out by multiplying by (1/2) to get the x on the left side and solved for the constant. Now your integral is (1/2)*(2x-2)/(9+(2x-2)^2)+4/(9+(2x-2)^2). The first term is a u substitution and the second term is your arctan.

 

[mike01]

Dick, Thanks for all your help and patientence but if the image attached repsents the original problem, and the problem + factoring / completing the square. Pardon my ignorance maybe I am just not seeing it but where is the (1/2) coming from? maybe it's just late here and I will look at it after a good nights rest. thanks for all your help, I am just trying to understand all this.

 

[Dick]

Here's the deal. To do the integrals you'll want to substitute basically u=(2x-2), right? That makes the denominator 3^2+u^2. I want to write the numerator x+3 in terms of u=(2x-2) as well. Solve u=(2x-2) for x. x=(1/2)*(u+2). Substitute that into x+3. (1/2)*(u+2)+3=(1/2)*u+4. That let's you split the integral into two parts. The (1/2)*u/(3^2+u^2) part is a simple sub. The 3/(3^2+u^2) is the arctan like part. See?