Integrating a squared velocity

[gendoikari87]

Okay I'm working on making a ballistics calculator and I need to know how to integrate this.

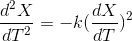To get velocity, and ultimately to get time of flight. So that I can use that to determine drop with an angle of 0.

 

[nasu]

Try to solve the equation in v first.
Replace dX/DT by v (on both sides).
You will have dv/dT=-kv^2. This can be solved by direct integration, after rearranging a little bit.

 

[rcgldr]

You will have dv/dT=-kv^2. This can be solved by direct integration, after rearranging a little bit.

Rearraging, this is what you would integrate, don't forget to include a constant after the integration (then solve for that constant based on initial conditions).

dv / (-k v²) = dt

 

[gendoikari87]

Rearraging, this is what you would integrate, don't forget to include a constant after the integration (then solve for that constant based on initial conditions).

dv / (-k v²) = dt

... that's just initial velocity is it not?

 

[rcgldr]

Don't forget to include a constant after the integration.

... that's just initial velocity is it not?

The integral will produce a function of velocity versus time, so the constant would be added or subtracted from the function of velocity at time = zero to account for the initial velocity.

 

[gendoikari87]

Rearraging, this is what you would integrate, don't forget to include a constant after the integration (then solve for that constant based on initial conditions).

dv / (-k v²) = dt

So this gives me:

1/kv+v_i=T correct?

From here I changed the V to dx/dt but since it is 1/v it becomes

(1/k)*dt/dx+V_i=T

Multiplying by dx I then get

(1/k)dt+V_idx=Tdx

Integrating yields

T/k +V_iX=T*X (accounting initial time and distance as zero)

But that just seems wrong...

Breaking it down all the way I get :

(V_i*X)/(x-1/k)=T

 

[nasu]

So this gives me:

1/kv+v_i=T correct?

No. Look at the units.
You add initial speed and inverse speed (times k).
It would be more obvious if you put it like
dv/v^2=-kdt
The integration on both sides gives
-1/v=-kt +C

At t=0 v=vi so
-1/vi=C or C=-1/vi
Then you have
1/v=1/vi+kt
Solve this for v and you have v(t).
Then you can integrate v(t) over time to get x(t).

 

[gendoikari87]

Cool, so I've solved for V:

V= 1/(KT+1/V_i)

Wolfram integrates it as

Log(KTV_i+1)/K=X

That doesn't seem right,

If I simply integrate KT+1/V_i with respect to X (because 1/v is dT/dX) I get

KTX+X/V_I=T

Which becomes

X/(V_i-KXV_i)=T

 

[nasu]

Cool, so I've solved for V:

V= 1/(KT+1/V_i)

Wolfram integrates it as

Log(KTV_i+1)/K=X

That doesn't seem right,

Why doesn't seem right?
Of course, you should add the constant that takes into account the initial position.

If I simply integrate KT+1/V_i with respect to X (because 1/v is dT/dX) I get

KTX+X/V_I=T

Which becomes

X/(V_i-KXV_i)=T

On the other hand, this does not seem right at all.
If you write
1/v=dt/dx=kt+1/vi
you have mixed variables (t and x). You cannot integrate right away.
After separation you have
dx=dt/(kt+1/vi) which seems to be same as above.

 

[gendoikari87]

Why doesn't seem right?
Of course, you should add the constant that takes into account the initial position.

call it intuition. I'll have to do unit analysis though. K I think has a dimention but IIRC it's inverse mass I'll check after while.

 

[nasu]

Sorry, I was editing my post while you posted your reply.
See above.

 

[nasu]

call it intuition. I'll have to do unit analysis though. K I think has a dimention but IIRC it's inverse mass I'll check after while.

The dimension of k is inverse length.And kt is inverse speed.

 

[gendoikari87]

Problem is the solution with the log function is giving me ansers of several thousand years for a flight time

This is where I get K, it's everything but the V squared term and divided by mass.

Edit: hold on, it could be my drag co-efficient is f'ed up.

 

[gendoikari87]

Yup, it was the BC, or at least i think, I'll have to check it out some more. Thanks for the help.

 

[nasu]

Problem is the solution with the log function is giving me ansers of several thousand years for a flight time

This may happen very well because you have only the drag force and no other forces.
After some time (and distance traveled) the speed will decrease practically to zero.
If your distance is much larger than the distance at which speed becomes very small, the time becomes very large. A plot of t(x) will show you better this behavior.
For example, taking vi=10 m/s and k=1m^-1, the time to travel 2 m is 0.6 s but the time to travel 20 m is of the order of 10^7 s (about a year).

 

[gendoikari87]

This may happen very well because you have only the drag force and no other forces.
After some time (and distance traveled) the speed will decrease practically to zero.
If your distance is much larger than the distance at which speed becomes very small, the time becomes very large. A plot of t(x) will show you better this behavior.
For example, taking vi=10 m/s and k=1m^-1, the time to travel 2 m is 0.6 s but the time to travel 20 m is of the order of 10^7 s (about a year).

Nah I was taking it at 100 meters. It was unit problem with the Drag coefficient converting from BC.