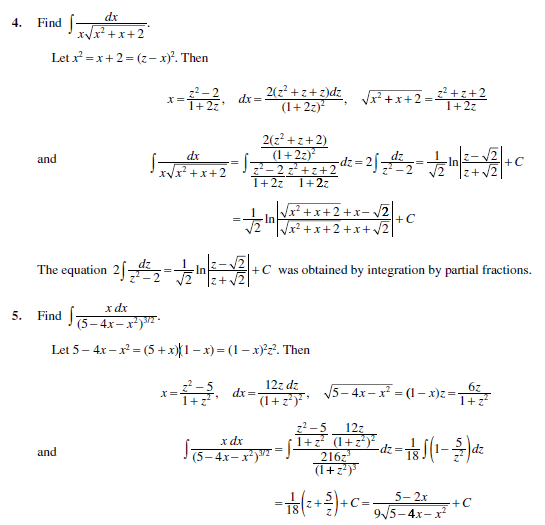Thanks for taking the time to answer my queries, I really appreciate it.
You are right, there are quite a few typos in the text. I guess my questions would be if:
$$ x^2 + x + 2 = (z-x)^2 $$ then: $$ \sqrt{x^2 + x + 2} = (z-x) $$ how did the author get: $$ \sqrt{x^2 + x + 2} = \frac {(z^2 + z + 2)} {1 + 2z} $$ also, how did he obtain x: $$ x = \frac {z^2 - 2} {1+2z} $$
The way I would attempt to solve it, is very tedious. Whilst the technique/substitution used by the author above seems to be very succinct and ingenious (if it works though).
My way would be as per the following (I probably made quite few errors along the way however, please let me know if the methodology used is wrong in principle, or if a better substitution can be used):
First complete the square of the quadratic in the square root:
$$ \int \frac {dx}{x + \sqrt{\left(x+\frac{1}{2}\right)^2 + \frac{7}{4}}} \,dx $$ then, set u to be: $$ u=x+\frac{1}{2} $$ hence, x would be: $$ x=u-\frac{1}{2} $$ therefore: $$ \int \frac {du}{u-\frac{1}{2} \sqrt{u^2 + \frac{7}{4}}} \,du $$ now replace u and du with: $$ \frac{\sqrt{7}}{2}\tan\theta = u $$ and $$ du =\frac{\sqrt{7}}{2} \sec^{2}\theta \, d\theta $$ Therefore, $$ \int \frac {\frac{\sqrt{7}}{2} \sec^{2}\theta}{\left(\frac{\sqrt{7}}{2}\tan\theta-\frac{1}{2} \right) \frac{\sqrt{7}}{2} \sec\theta} \,d\theta $$ simplifying: $$ =\int \frac {\sec\theta}{\frac{\sqrt{7}}{2}\tan\theta-\frac{1}{2}} \,d\theta $$ further simplifying: $$ =\int \frac {d\theta}{\frac{\sqrt{7}}{2}\sin\theta-\frac{1}{2}\cos\theta} $$ from here the only substitution I can think of is to set: $$ \tan\frac{\theta}{2}=t \ $$ then, using the double angle trig identity we have: $$ \cos\theta= \frac{1-t^2}{1+t^2} \text{, } \sin\theta= \frac{2t}{1+t^2} $$ differentiating the inverse tan, we get: $$ d\theta= \frac {2}{1+t^2} dt $$ substituting in our integral, we have: $$ =\int \frac {\frac {2}{1+t^2} dt}{\frac{\sqrt{7}}{2}\frac{2t}{1+t^2}-\frac{1}{2}\frac{1-t^2}{1+t^2}} $$ Simplifying: $$ =\int \frac {4dt}{2\sqrt{7}t-1+t^2} $$ Solving the quadratic, we have: $$ =\int \frac {4dt}{\left(t+\sqrt{7}+2\sqrt{2}\right)\left(t+\sqrt{7}+2\sqrt{2}\right)} $$ and then using partial fraction decomposition, we have: $$ =\frac{1}{\sqrt{2}}\int \frac {dt}{t+\sqrt{7}-2\sqrt{2}} - \frac{1}{\sqrt{2}}\int \frac {dt}{t+\sqrt{7}+2\sqrt{2}} $$ finally, integrating: $$ =\frac{1}{\sqrt{2}}\ln\left|t+\sqrt{7}-2\sqrt{2} \right| - \frac{1}{\sqrt{2}}\ln\left|t+\sqrt{7}+2\sqrt{2} \right| $$ simplifying: $$ =\frac{1}{\sqrt{2}}\ln\left|\frac {{t+\sqrt{7}-2\sqrt{2}}}{t+\sqrt{7}+2\sqrt{2}} \right| $$ remembering that: $$ \theta = \tan^{-1}\left( \frac{2u}{\sqrt{7}}\right) $$ substituting: $$ =\frac{1}{\sqrt{2}}\ln\left|\frac {{\tan\frac{\theta}{2}+\sqrt{7}-2\sqrt{2}}}{\tan\frac{\theta}{2}+\sqrt{7}+2\sqrt{2}} \right| $$ remembering that: $$ \theta = \tan^{-1}\left( \frac{2u}{\sqrt{7}}\right) $$ substituting: $$ =\frac{1}{\sqrt{2}}\ln\left|\frac {{\tan\left(\frac{\tan^{-1}\left( \frac{2u}{\sqrt{7}}\right)}{2}\right)+\sqrt{7}-2\sqrt{2}}}{\tan\left(\frac{\tan^{-1}\left( \frac{2u}{\sqrt{7}}\right)}{2}\right)+\sqrt{7}+2\sqrt{2}} \right| $$ finally, remembering that: $$ x=u-\frac{1}{2} $$ substituting: $$ =\frac{1}{\sqrt{2}}\ln\left|\frac {{\tan\left(\frac{\tan^{-1}\left( \frac{2x+1}{\sqrt{7}}\right)}{2}\right)+\sqrt{7}-2\sqrt{2}}}{\tan\left(\frac{\tan^{-1}\left( \frac{2x+1}{\sqrt{7}}\right)}{2}\right)+\sqrt{7}+2\sqrt{2}} \right| $$
Again, I am sure I made mistakes along the way, however is my method correct in principle. Also, do you have any other suggestion or can figure out what the text author is doing?