- 29,123
- 4,541
Perhaps it is known to you, it was something new to me.
After Andy confirmed that reasonable circle of confusion for my camera should be about 0.02mm, I did some calculations - and I was surprised by the result.
Say you have an object that you want to take a picture of (be it flower, book, chair - something like that). Say its size is x cm and you want it to fit whole frame. What focal length lens should you use to get the largest DOF (assuming f-number of 8, as it usually gives best results)?
The answer is... it doesn't matter! Well, almost doesn't matter:
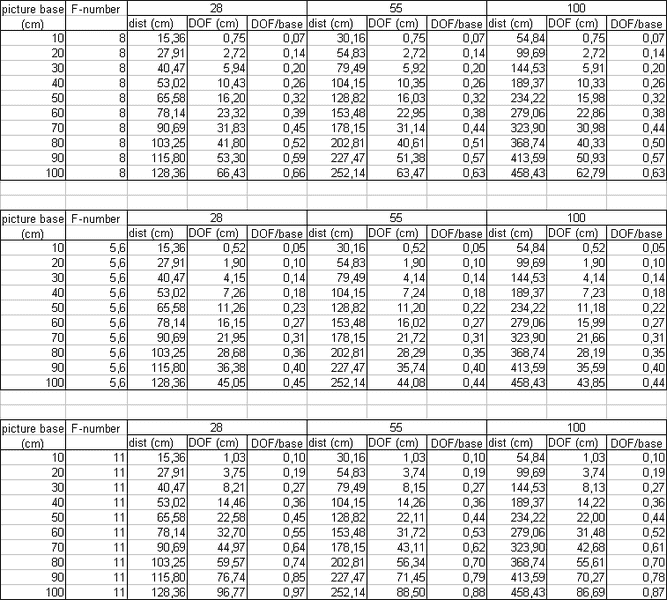
Note how for a given size of the object DOF/base ratio is always the same, no matter what focal length you use. For example - 30 cm object, f-number of 8, DOF/object size is always 0.20.
Picture base is a width of the object, dist is a distance between object and the sensor (for obvious reasons it changes with the focal length), DOF/base is the ratio between DOF and object size - and it turns out this ratio almost doesn't depend on the focal length. At least as long as we are talking about relatively small objects up to 1 meter. Shorter focal lengths give marginally larger DOF - that's what I expected, but I expected the difference to be much larger. Turns out short focal length means you have to get close to the object, and DOF gets smaller - so there is no gain.
After Andy confirmed that reasonable circle of confusion for my camera should be about 0.02mm, I did some calculations - and I was surprised by the result.
Say you have an object that you want to take a picture of (be it flower, book, chair - something like that). Say its size is x cm and you want it to fit whole frame. What focal length lens should you use to get the largest DOF (assuming f-number of 8, as it usually gives best results)?
The answer is... it doesn't matter! Well, almost doesn't matter:
Note how for a given size of the object DOF/base ratio is always the same, no matter what focal length you use. For example - 30 cm object, f-number of 8, DOF/object size is always 0.20.
Picture base is a width of the object, dist is a distance between object and the sensor (for obvious reasons it changes with the focal length), DOF/base is the ratio between DOF and object size - and it turns out this ratio almost doesn't depend on the focal length. At least as long as we are talking about relatively small objects up to 1 meter. Shorter focal lengths give marginally larger DOF - that's what I expected, but I expected the difference to be much larger. Turns out short focal length means you have to get close to the object, and DOF gets smaller - so there is no gain.