christof6869
- 5
- 0
So I've been working on this for a while now, but I'm a little stuck. I think I see how to solve the problem below, just need a couple tips to get me over the hurdle.
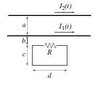
There are two infinite wires in the same plane as a rectangular loop. Geometries are displayed in the attached figure. The two wires have currents of known relationship to time I1(t)= I1i+ut and I2(t)= I2i+vt, where u, v, I1i and I2i are all time-independent values. The loop has a known resistance R.
What is the induced current in the wire loop?
Magnetic field created by current in a wire
B=μI/2πr (r is the distance from the wire to the loop)
EMF= -A(dB/dt) (A is the area of the loop cd)
Iinduced=EMF/R
I know the current induced is the induced EMF divided by resistance of loop R. To find EMF, I need to use Faraday's law, where the EMF induced is the change in magnetic flux times change in time. Since area is constant, only magnetic field changing in time causes the change in flux.
Here's where I have my problem. I don't know how to quantify the magnetic field. Ampere's law let's me use the following relationship.
B=μI/2πr
I'm pretty sure that the field strength falls off as you move farther away from the wire, so it has distance dependence (thus the r variable) as well as time dependence. So which distance do I use? If I take wire 1, the distance from the loop is b, but I need to account for the distance b + c. Is there some sort of average magnetic field going through the loop?
Homework Statement
There are two infinite wires in the same plane as a rectangular loop. Geometries are displayed in the attached figure. The two wires have currents of known relationship to time I1(t)= I1i+ut and I2(t)= I2i+vt, where u, v, I1i and I2i are all time-independent values. The loop has a known resistance R.
What is the induced current in the wire loop?
Homework Equations
Magnetic field created by current in a wire
B=μI/2πr (r is the distance from the wire to the loop)
EMF= -A(dB/dt) (A is the area of the loop cd)
Iinduced=EMF/R
The Attempt at a Solution
I know the current induced is the induced EMF divided by resistance of loop R. To find EMF, I need to use Faraday's law, where the EMF induced is the change in magnetic flux times change in time. Since area is constant, only magnetic field changing in time causes the change in flux.
Here's where I have my problem. I don't know how to quantify the magnetic field. Ampere's law let's me use the following relationship.
B=μI/2πr
I'm pretty sure that the field strength falls off as you move farther away from the wire, so it has distance dependence (thus the r variable) as well as time dependence. So which distance do I use? If I take wire 1, the distance from the loop is b, but I need to account for the distance b + c. Is there some sort of average magnetic field going through the loop?